摘要：我們使用近似的物理光學(xué)模模擬了半徑的測(cè)量。使用簡(jiǎn)單的幾何光線模型替換復(fù)雜的物理光學(xué)模型，可以確定在測(cè)量中的偏差。
1. 簡(jiǎn)介
半徑干涉測(cè)量通常通過(guò)簡(jiǎn)單的幾何模型來(lái)模擬，即，來(lái)自物鏡（或標(biāo)準(zhǔn)透鏡）的光線形成錐形并且聚焦到一點(diǎn)[1]。當(dāng)測(cè)試光學(xué)器件變小和/或需要更高的精度時(shí)，這個(gè)簡(jiǎn)單的幾何模型就會(huì)產(chǎn)生問(wèn)題并得到錯(cuò)誤的半徑測(cè)量值。需要完整的物理光學(xué)模型來(lái)捕獲系統(tǒng)的衍射效應(yīng)和像差。
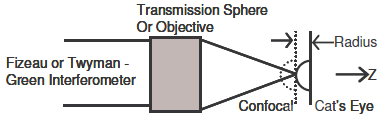
半徑干涉測(cè)量的原理圖如圖1所示。菲索或泰曼格林干涉儀都可用于半徑測(cè)量。在菲索干涉儀中，標(biāo)準(zhǔn)透鏡用作聚焦元件、分束和參考表面。在泰曼格林干涉儀中，使用分束器將光分成參考反射鏡和物鏡，它可以將光束聚焦到測(cè)試部件。
通過(guò)首先將部件放置在共焦位置，然后將部件移動(dòng)到貓眼位置，并測(cè)量部件移動(dòng)的距離，來(lái)測(cè)量測(cè)試部件的半徑，該距離就是測(cè)試部件的半徑。當(dāng)澤尼克多項(xiàng)式[1]的離焦項(xiàng)為零時(shí)，共焦和貓眼位置重合。在視覺(jué)上，靶心環(huán)是空的。因?yàn)椴僮髡卟荒軐⒉考䴗?zhǔn)確地放置在所需的位置，所以用于確定共焦和貓眼位置的最準(zhǔn)確的方法是逐步通過(guò)這兩個(gè)位置。當(dāng)操作者以小步幅移動(dòng)部件通過(guò)共焦和貓眼時(shí)，我們記錄離焦和Z位置。然后，我們用一條線擬合離焦VS.Z位置。共焦和貓眼位置是Z位置軸上的截距。這種通過(guò)共焦和貓眼步進(jìn)的方法可用于精確半徑測(cè)量[2]，我們?cè)谶@里用于半徑測(cè)量的模擬。
圖1：半徑干涉測(cè)量幾何模型原理圖
在NIST的精密半徑干涉測(cè)量實(shí)驗(yàn)顯示了標(biāo)稱24.466mm半徑的Zerodur球的測(cè)量之間的差異。球體由坐標(biāo)測(cè)量?jī)x機(jī)械測(cè)量，同時(shí)在使用不同標(biāo)準(zhǔn)透鏡的干涉儀上光學(xué)測(cè)量[2]。即使考慮了測(cè)量中的所有已知偏差和不確定性，這種在75nm至400nm范圍內(nèi)的差異仍然存在。對(duì)于這種差異的解釋可能是光被假定遵循幾何模型而不是更準(zhǔn)確的物理光學(xué)模型，我們將在這里進(jìn)行測(cè)試。
在光的幾何模型中，當(dāng)透鏡的頂點(diǎn)與光的焦點(diǎn)（發(fā)生在距離聚焦元件一個(gè)焦距處）重合時(shí)，就會(huì)出現(xiàn)貓眼位置。然后，共焦位置距離貓眼位置一個(gè)半徑。在非像差幾何模型中，這發(fā)生在聚焦元件的波前的曲率等于測(cè)試部件的曲率時(shí)。
半徑測(cè)量的高斯模型表明了當(dāng)使用幾何模型而不是更復(fù)雜的高斯模型時(shí)，半徑測(cè)量中存在誤差[3]。對(duì)于較小的半徑部分（<1mm），這個(gè)誤差是在105部件的量級(jí)，而對(duì)于較大的部件（25mm），有接近108部件的誤差。當(dāng)考慮具有半徑像差的高斯模型時(shí)，NIST [2]的研究者發(fā)現(xiàn)了6nm的誤差（107部件）。這些像差是由標(biāo)準(zhǔn)透鏡和系統(tǒng)中的其他光學(xué)元件的缺陷引起的。
下一步是考慮物理光學(xué)模型。當(dāng)然，焦點(diǎn)區(qū)域的分析計(jì)算是不可行的，因此需要近似。對(duì)于這種物理光學(xué)模型，我們使用來(lái)自Photon Engineering的軟件包FRED [4]。
2. FRED模型
FRED通過(guò)將光源光束近似為點(diǎn)網(wǎng)格來(lái)近似物理光學(xué)模型，其中每個(gè)點(diǎn)發(fā)出高斯分布“子束”。 每個(gè)高斯子束以ABCD矩陣方法[5]傳輸通過(guò)光學(xué)系統(tǒng)。在每個(gè)子束通過(guò)系統(tǒng)之后，疊加“探測(cè)器”上子束的波前，以近似物理光學(xué)模型。FRED是一個(gè)可視化軟件包，其中透鏡、反射鏡和光源都顯示在它們的相對(duì)位置。FRED不執(zhí)行幾何分析。
為了模擬半徑測(cè)量，我們首先插入每個(gè)元件（光源、聚焦透鏡、測(cè)試部件和探測(cè)器）到FRED文件中。然后追跡來(lái)自光源的光線。光線由聚焦元件聚焦，從測(cè)試部分反射，再由聚焦元件準(zhǔn)直，然后在探測(cè)器處讀取。在探測(cè)器處的期望輸出是波前的相位。我們按照所述步驟通過(guò)共焦和貓眼位置，并獲得每個(gè)點(diǎn)的相位圖。然后我們使用Matlab讀取相位數(shù)據(jù)和Z位置，以確定共焦和貓眼的位置。半徑是兩個(gè)位置之間的差，半徑誤差是測(cè)試部件的輸入半徑和輸出半徑之間的差。
我們?cè)谀M半徑測(cè)量中使用了兩個(gè)不同的光源。我們測(cè)試了在整個(gè)圓形孔徑上具有恒定強(qiáng)度和相位的圓形孔徑光束，這模擬了最佳實(shí)驗(yàn)裝置。第二個(gè)光源是高斯強(qiáng)度光束，通過(guò)改變子束的強(qiáng)度，使得強(qiáng)度的疊加是高斯分布，來(lái)形成該高斯光束。光源波長(zhǎng)為632.8nm（氦-氖），并設(shè)置為相干。子束的數(shù)量可以改變，并且影響測(cè)量的時(shí)間和輸出相位。我們測(cè)試了不同孔徑尺寸的光源，從直徑為4mm的微干涉儀到直徑為150mm的大尺度干涉儀。
我們測(cè)試了兩種類型的聚焦元件。因?yàn)镕RED使用實(shí)際光學(xué)器件而不是近軸近似，所以典型的透鏡具有太多的附加的球差。因此，我們首先使用拋物面作為聚焦元件，接下來(lái)使用具有圓錐表面（以減少像差）的透鏡作為聚焦元件。我們通過(guò)改變焦距來(lái)測(cè)試不同的數(shù)值孔徑。
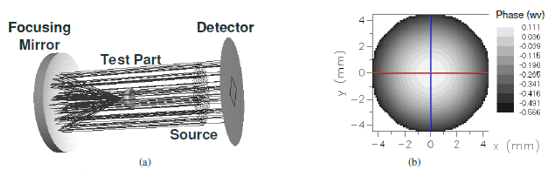
我們測(cè)試了一系列測(cè)試部件，半徑從0.25mm到1mm，用于微干涉儀裝置，半徑25mm附近，用于宏觀干涉儀。模擬探測(cè)器以像素劃分，且可以改變。使用的像素越多，測(cè)量速度就越慢，并會(huì)影響相位輸出。圖4（a）示出了使用拋物面聚焦元件的示例測(cè)量。圖4（b）是當(dāng)部件位于貓眼附近時(shí)的波前相位圖的圖片。主要的誤差是離焦，這表明部件并不完全在貓眼處。
圖4.（a）FRED中半徑測(cè)量示意圖（b）來(lái)自FRED波前相位示例
3. 結(jié)果
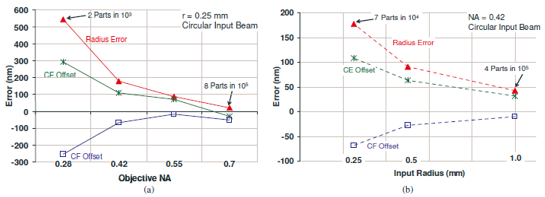
由于篇幅限制，此處僅顯示了幾個(gè)結(jié)果。該模型顯示了半徑、貓眼位置和共焦位置處的誤差。也就是說(shuō)，輸出半徑不等于輸入半徑，并且貓眼和共焦位置會(huì)有偏移。圖5顯示出對(duì)于改變NA和部件尺寸而沒(méi)有附加的像差的微干涉儀的模型的結(jié)果。如圖5（a）所示，誤差隨著的NA目標(biāo)變小而增加，如預(yù)期的那樣，因?yàn)榻裹c(diǎn)較大。此外，對(duì)于較大的部件，誤差較小，如圖5（b）所示。對(duì)于在f/3.2和25mm半徑輸入部件的宏觀尺度干涉儀，誤差為133nm，106中5個(gè)部件。這個(gè)誤差量可以開始解釋在NIST的實(shí)驗(yàn)中所顯示的差異[2]。這些誤差不存在任何像差。如果將典型的像差量添加到模型中，則預(yù)期誤差將增加，這是我們的工作的下一環(huán)節(jié)。
圖5.使用幾何模型而不是更加復(fù)雜的FRED模型的誤差，數(shù)據(jù)來(lái)源于微干涉儀裝置。
4. 討論和總結(jié)
我們預(yù)測(cè)模型假設(shè)將會(huì)在焦點(diǎn)區(qū)域附近受到挑戰(zhàn)，有時(shí)稱為焦散。在焦散點(diǎn)附近，射線不垂直于波前，以及“相位偏移”[6]，即使對(duì)于無(wú)像差波前也是如此。因此，波場(chǎng)的分析具有誤差。最近的一篇出版物很好地總結(jié)了情況，“對(duì)在不同介質(zhì)之間的彎曲界面處具有焦散的波場(chǎng)的分析仍然是一個(gè)重大挑戰(zhàn)...我們不知道任何現(xiàn)有的基于光線的模型可以分析這種情況”[7]。彎曲界面是半徑測(cè)量中的測(cè)試部件。為了解決這個(gè)問(wèn)題，作者提出修改軟件中的高斯子束源來(lái)解決這個(gè)問(wèn)題。這種用于光學(xué)建模的方法顯然不在本工作的范圍內(nèi)，而是在此介紹FRED中的誤差并作為未來(lái)研究的方向。
我們進(jìn)行了有限的不確定性分析。第一個(gè)不確定性是散焦對(duì)位置圖擬合的不確定性，其由模型故障、解包算法中的誤差、相機(jī)的像素特性和澤尼克擬合算法中的誤差引起。由擬合引起的半徑不確定性有波動(dòng)，但對(duì)于大多數(shù)情況可以估計(jì)在±40nm。FRED模型中的另一個(gè)不確定性來(lái)源是選擇輸入光線子束的數(shù)量和相機(jī)中的像素?cái)?shù)量。這些選擇導(dǎo)致輸出半徑中的±31nm（光源）和±64nm（探測(cè)器器）的不確定性。我們使用簡(jiǎn)單的和的平方根法來(lái)組合這三個(gè)不確定性來(lái)源，以估計(jì)來(lái)自FRED模型的半徑的不確定性為±81nm。因?yàn)檫@種不確定性很大，F(xiàn)RED不太可能用于校正在幾何模型中沒(méi)有考慮的高精度的偏差，但是我們?nèi)匀豢梢允褂肍RED尋找趨勢(shì)。
我們指出，當(dāng)使用簡(jiǎn)單幾何模型而不是更復(fù)雜的物理光學(xué)模型時(shí)，在半徑干涉測(cè)量中存在誤差。該誤差隨著部件半徑的減小和物鏡NA的減小而增加。這個(gè)誤差可能有助于解釋一些實(shí)驗(yàn)結(jié)果中發(fā)現(xiàn)的差異。但是，物理光學(xué)模型的近似不是完美的，也具有不確定性。這種不確定性使得軟件不可能用于校正測(cè)量中的偏差。該軟件可用于顯示由使用幾何模型而不是物理光學(xué)模型引起的不確定性的大小。
5. 參考文獻(xiàn)
[1] J. Breivenkamp and J.Bruning, “Phase Shifting Interferometry,” in Optical Shop Testing, D. Malacara, ed. (John Wiley and Sons, Inc., NY,1992), 501-598.
[2] T.L. Schmitz, A.D. Davies, and C.J. Evans, “Uncertainties in interferometric measurements of radius of curvature,” in Optical Manufacturing and Testing IV, H.P. Stahl, Ed., Vol. 4451 of Proceedings of SPIE (SPIE, Bellingham, WA, 2001), 432-447.
[3] K. M. Medicus, Improving Measurements Based on the Cat’s Eye Retro-Reflection, Diss., (UNC Charlotte, Charlotte, NC 2006).
[4] Photon Engineering, 440 South Williams Blvd., Suite # 106 Tucson, Arizona 85711, 520-733-9557.
[5] Jacques Arnaud, “Representation of Gaussian beams by complex rays,” Applied Optics, 24, 538-543, (1985).
[6] G.W. Forbes and M.A. Alonso, “Using rays better. I. Theory for smoothly varying media,” JOSA, 18, 1132-1145, (2001).
[7] G.W. Forbes and M.A. Alonso, “Using rays better. III. Theory for smoothly varying media,” JOSA, 18, 1357-1370, (2001).
文章來(lái)源：Medicus, Kate M., and A. Davies. "Physical Optics Modeling of the Interferometric Radius Measurement." Optical Fabrication and Testing2006
|
