SITE ZHANG,1,2,*CHRISTIAN HELLMANN,2 AND FRANK WYROWSKI1
1Applied Computational Optics Group, Institute of Applied Physics, Friedrich Schiller University Jena, Max-Wien-Platz 1, 07743 Jena, Germany
2Wyrowski Photonics UG, Kahlaische Straße 4, 07745 Jena, Germany
*Corresponding author: site.zhang@uni‑jena.de
Received 8 March 2017; revised 29 April 2017; accepted 3 May 2017; posted 3 May 2017 (Doc. ID 290298); published 19 May 2017
Received 8 March 2017; revised 29 April 2017; accepted 3 May 2017; posted 3 May 2017 (Doc. ID 290298); published 19 May 2017
ͨ�^(gu��)ʹ��ƽ�沨�V�����Լ�S��ꇷ������҂��о���һ��늴ň�(ch��ng)��(j��ng)�^(gu��)�ɸ���ͬ�Խ��|(zh��)���߸����Խ��|(zh��)��(g��u)�ɵĹ�W(xu��)�Ӡ�Y(ji��)��(g��u)�Ă������҂�߀�_(k��i)�l(f��)��һ�N���ڿ��ٸ����~׃�Q���g(sh��)���㷨�����Д�(sh��)ֵ��Ч�IJɘ�Ҏ(gu��)�t��ͨ�^(gu��)�����㷨�c����ϵ�y(t��ng)��ģ���g(sh��)��Y(ji��)�ϣ��҂�չʾ��һЩ���永�����罛(j��ng)�^(gu��)һ��(g��)����ͬ�Է����(bi��o)��(zh��n)�ߵĹ��(ch��ng)��ݔ�Լ��������ⷽλ���S����Ć��S���wƽ��Ĺ��(ch��ng)��ݔ��
OCIS codes: (260.0260) Physical optics; (260.2110) Electromagnetic optics; (260.1440) Birefringence; (230.4170) Multilayers.
https://doi.org/10.1364/AO.56.004566
1.����
��ƽ��ƽ�昋(g��u)�ɵĹ�W(xu��)���ڹ�W(xu��)�ЏV����(y��ng)�á��Ӡ�Y(ji��)��(g��u)���������S�ͬ��r��ģ�ͣ���ƽ��͘�(bi��o)��(zh��n)�ߡ������@��(g��)��(sh��)�����c�Ӡ�Y(ji��)��(g��u)����õ����}һֱ�����ҵ�ע�Ⲣ�Ҍ�(du��)���ѽ�(j��ng)�M(j��n)���˴������о���
���@�(l��i)�о��У������(sh��)�^�c(di��n)����(c��)����ƽ�沨��Ȼ���H�H�ٔ�(sh��)���о�ʹ����ƽ�沨�V������SPW����(l��i)���]һ���늴ň�(ch��ng)�����磬�����īI(xi��n)[1-6]���о��˸���ͬ��-����ͬ�ԵĽ����ϣ���˹�����ķ����ʺ����ʣ��څ����īI(xi��n)[7-11]���о��˸���ͬ�Ԍӻ���ƽ�����r�������īI(xi��n)[12-22]ӑՓ�˸���ͬ��-�����Խ������r���څ����īI(xi��n)[23-26]�ЄtӑՓ�˸����Ԍӻ���ƽ�����r��
�������ᵽ���S���о��������ض����о����}����[1,3,5]���о��˸�˹����ȫ��(n��i)����ęM��ƫ�ƣ��������������P(gu��n)ע�ھ��w�����á���ˣ����@Щ�����ƏV����һ�����r�Ŀ������ܵ������ơ�
���@ƪ�����У��҂���һ��(g��)��һ����^�c(di��n)��(l��i)���]�ˆ�(w��n)�}����W(xu��)�ӎ�����(hu��)�Ϊ�(d��)ʹ�ã��෴������������һ��(g��)��W(xu��)ϵ�y(t��ng)��һ���ֲ��Һ�������Ԫ��һ��ʹ�ã���D1����ʾ�����ڴ���(sh��)���҂���ѭ��(ch��ng)�E�ĸ���[27]����ʹ�ò�ͬ�Ĉ�(ch��ng)�E���ӽM��[28-32]����D1����ʾ���Ԍ�(du��)һ��(g��)�����ˌӽ��|(zh��)Ԫ����ϵ�y(t��ng)�M(j��n)��������W(xu��)ģ�M�����]��ģ�M�nj�(du��)����(g��)ϵ�y(t��ng)�����dž�(g��)Ԫ��������ӽY(ji��)��(g��u)����cϵ�y(t��ng)��ǰ�����B�ӡ��@Ҫ���҂��������E���D1�е�P���M(j��n)���m��(d��ng)?sh��)Ŀ��]����ǰһ��(g��)Ԫ����ݔ���B�ӵ���(d��ng)ǰԪ����ݔ�룬������(d��ng)ǰԪ����ݔ�����f����һ��(g��)Ԫ����һ����r�£��@�ӵĂ�ݔ���E��(hu��)���F(xi��n)��ƽ�л��߷�ƽ��ƽ��֮�g���څ����īI(xi��n)[28,29]���ѽ�(j��ng)�ᵽ��ƽ��ƽ���g�N��Ч�Ă�ݔ�������څ����īI(xi��n)[33]�Єt�����ҵ���(du��)��ƽ��ƽ���g��ݔ?sh��)�һ��(g��)Ԕ��(x��)��ӑՓ�����@ƪ�����У��҂�����(hu��)�о���ݔ���E������(hu��)�P(gu��n)ע�Ӡ�Y(ji��)��(g��u)��Ԫ������C��
���⣬�Ĕ�(sh��)ֵӋ(j��)����^�c(di��n)���l(f��)�����ˈ�(zh��)��һ��(g��)�B�m(x��)����Ч��ϵ�y(t��ng)ģ�M��Ҫ��Ԫ������C
���_��̎���ɘӈ�(ch��ng)��(sh��)��(j��)����������������һ�N�y(t��ng)һ�ĸ�ʽ���f��(ch��ng)��(sh��)��(j��)��
��(y��u)����(sh��)ֵӋ(j��)���Ч�ʡ�
���]�������ɂ�(g��)��(bi��o)��(zh��n)���҂��_(k��i)�l(f��)��һ�N�����Ԅ�(d��ng)��(sh��)ֵ�ɘ�Ҏ(gu��)�t��SPW�������c֮ǰһЩ���÷e�ַ�����(du��)���g�ͽ��V���P(gu��n)�ĸ����~׃�Q�M(j��n)�u(p��ng)�����о���ȣ��煢���īI(xi��n)[23]�еĶ��S���c(di��n)Ҏ(gu��)�t�ͅ����īI(xi��n)[12-14��20��25]�е�Stamnes–Spjelkavik–Pedersen����[34]�����҂�ʹ���˿��ٸ����~׃�Q��FFT�����g(sh��)���˼��g(sh��)�ڴ�?j��n)?sh��)ֵܛ�����������L��(w��n)����Ч�ʸߡ��ټ����ڽ��V���н�(j��ng)�^(gu��)���뿼�]�Ĕ�(sh��)ֵ�ɘ�Ҏ(gu��)�t���҂��ķ�������һ���m���ԣ���(du��)��Ԫ���������(ch��ng)�](m��i)���κ����ơ���ˣ����㷨����ֱ�Ӱ�����һ��(g��)������W(xu��)ϵ�y(t��ng)ģ�M֮�С�
�D1.�Y(ji��)��ʹ�ò�ͬ�Ĉ�(ch��ng)ۙ���Ӂ�(l��i)ģ�M��W(xu��)ϵ�y(t��ng)�� C��Ԫ�����ӣ�P������Ԫ��֮�g�Ă�ݔ���ӡ�
2.��Փ
��D2��ʾ���Ӡ�Y(ji��)��(g��u)�քe�Ƀɂ�(g��)λ�� 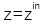 �� 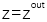 ��ƽ��ƽ�昋(g��u)�ɡ� 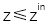 �� 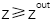 �ą^(q��)���M�ˏ�(f��)�����ʞ� 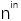 �� 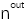 �ľ������ͬ�Խ��|(zh��)�������īI(xi��n)[27]�б���ʹ�ÙM�����Ex��Ey���������������ͬ�Խ��|(zh��)��늴ň�(ch��ng)�ˡ���ˣ��҂�����ʹ�����±��_(d��)ʽ��(l��i)�����ˆ�(w��n)�}��
���У��քe��ƽ�� 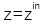 �� 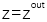 ̎���xݔ���ݔ���M��늈�(ch��ng)ʸ����������λ�ڽ���Ĕ�(sh��)�W(xu��)λ�ã��������J(r��n)���ھ�����|(zh��)��һ��(c��)��������ʽ�o��
���� 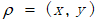 �����̣�1���е�Ԫ��������һ��(g��)2x2�ľ����ʽ��
�D2.�Ӡ�Y(ji��)��(g��u)�քe�Ƀɂ�(g��)λ�� 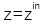 �� 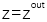 ��ƽ��ƽ�昋(g��u)�ɡ� 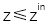 �� 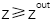 �ą^(q��)���ɾ������ͬ�Խ��|(zh��)��䣬�������ʷքe�� 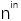 �� 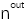 ��ݔ����(ch��ng)��ݔ����(ch��ng)�ڌӱ����M(j��n)�ж��x��������������(y��ng)�ĸ���ͬ�Խ��|(zh��)��һ��(c��)��
���@�¹�(ji��)���҂���Ŀ��(bi��o)���ҵ�C�ľ��_����ʽ�����B�ӌӽ��|(zh��)Ԫ����ݔ���ݔ����(ch��ng)�������о��c�ӽY(ji��)��(g��u)������ã��҂���(du��)ݔ��M���(ch��ng)�����M(j��n)����һ��(g��)�����~׃�Q�����@����
���� 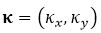 , F��ʾ���S�����~׃�Q��
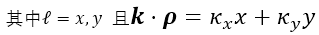 ���渵���~׃�Q���x����
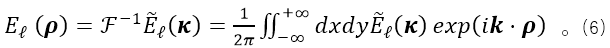
���̣�6���еķe�ֿ��Խ�ጞ錢 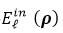 �ֽ����в�ͬ�M��ʸ����κ��ƽ�沨����ˣ����҂�����r�£�ÿ��(g��)ݔ��ƽ�沨�����ԆΪ�(d��)̎��——�҂�����Ӌ(j��)��ÿ��(g��)ݔ��ƽ�沨��ݔ����Ȼ���M(j��n)����͏Ķ��@��ݔ����(ch��ng)��
���⣬����(j��)߅��l����(du��)늴ň�(ch��ng)ʩ�ӵ��B�m(x��)��Ҫ�����@ʾ��һ��(g��)�o����ݔ��ƽ�沨���c�ӽY(ji��)��(g��u)����õ��^(gu��)������M��ʸ����κ�ض����ֲ�׃��ͬ�ӿ����@ʾ����ͨ�^(gu��)�B��ԭ������Ч�ԣ���ͬ��κ֮�g�](m��i)����ϡ���ˣ���(du��)��ݔ�����V���҂����Ԍ�(xi��)��
����
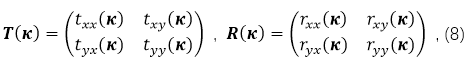
��ʽ��8���зքe����ͷ���ϵ��(sh��)��ꇡ�����Ӌ(j��)��T(κ) ����R(κ)���҂��x��ʹ�Ô�(sh��)ֵ��(w��n)��S��ꇷ���������Ӌ(j��)��S��ꇣ����ȱ�횴_��ÿ��(g��)�����Ԍӵ�ƽ�沨�������īI(xi��n)[35]��Berreman��4x4��ꇹ�ʽ��Landry��Maldonado�_(k��i)�l(f��)��չʾ��һ�N��(sh��)ֵ�Ѻõ���ʽ��Ҋ(ji��n)�����īI(xi��n)[23]���҂������������ķ�������(du��)��ÿһ�ӣ�����˅����īI(xi��n)[23]���ɷ��̣�28��������������ϵ�y(t��ng)������ֵ������������
��ͬ��[23��25]��ֱ��ʹ�ñ������(l��i)��(g��u)��һ��(g��)�D(zhu��n)�Q��ꇣ����⣬�҂�߀��Ҫ����(j��)�����Ă�ݔ����������ƽ�沨���@�Ǟ�Ӌ(j��)��S���������һ��(g��)����Ĝ�(zh��n)�䡣��ˣ��҂���ѭ[36]��4.3������Li������Ę�(bi��o)��(zh��n)��
Ȼ����ԑ�(y��ng)���f�wS��ꇹ�ʽ���҂�?c��)��@ƪ���в����؏�(f��)�o���Ѱl(f��)չ�����S��ꇷ������x�߿��ԅ����īI(xi��n)[37]�еķ��̣�5��-��8���ԫ@�ø������Ϣ�����҂�����r�У����ڛ](m��i)�з����ݔݔ���(ch��ng)���҂��H��(du��)��������߷�������dȤ������@ƪ�����еľ��ϵ��(sh��)T(κ) ��R(κ)��(du��)��(y��ng)��[37]�з��̣�5c�����ߣ�5d���е��Ӿ��T_uu ����R_du��
һ���@���˾��ϵ��(sh��)��ͨ�^(gu��)����(7)���ɫ@��ݔ�����V����(du��)ݔ�����V�M(j��n)��һ��(g��)�渵���~׃�Q���҂��@����ݔ���M���(ch��ng)ʸ��
ͨ�^(gu��)(li��n)�Ϸ��̣�4������7������9�����҂����Ԍ�(xi��)����ݔ���(ch��ng)��ݔ����(ch��ng)����(g��)Ӌ(j��)�����̣����
�҂��������r�������ӣ��t
��ˣ����̣�1����Ԫ������C�ľ��_��ʽ����
ͨ�^(gu��)ʹ��ϵ��(sh��)���R(κ)���� T(κ)�����ԫ@�÷�����r�ı��_(d��)ʽ��
3.�㷨
���շ��̣�10��������҂����ԑ�(y��ng)��һ�N��(sh��)ֵ�㷨��Ӌ(j��)���(ch��ng)��(j��ng)�^(gu��)�ӽ��|(zh��)Ԫ���Ă�ݔ���҂��ęM��ݔ���(ch��ng)ʸ�� 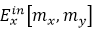 �� 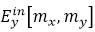 ���ԈD3��a���еľ���W(w��ng)���M(j��n)�вɘӡ��@�N�W(w��ng)���x�� 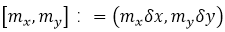 ,���� 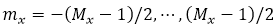 �� 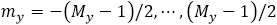 ����������(sh��)��δx��δy��x�����y����IJɘӾ��x����ʼ�ɘӅ���(sh��)��(y��ng)ԓ�ܵ����m�Ŀ�����ʹ����������ǰ���ӵ��ο�˹��-���r(n��ng)�ɘӶ��������̣�10���е�F��(li��n)ϵ���g����l��������ӣ�����ʹ�ò�ͬ�Ĕ�(sh��)ֵ������(sh��)�F(xi��n)����V��ʹ�õĿ��ٸ����~׃�Q��FFT�����g(sh��)���Լ��������܉��M(j��n)һ����ߔ�(sh��)ֵЧ�ʵİ���������~׃�Q[38]�����z׃�Q[39-41]�ĸ���(j��)�ķ������ڴ�ƪ�����У��҂�ʹ����FFT���g(sh��)�����Դ˫@��ݔ����V�����҂����㷨��������ԓ���g(sh��)��
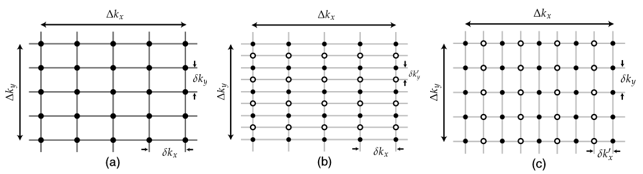
�D3.�ڽ��V���x����ɘӾW(w��ng)��a������ʼ�W(w��ng)���x��5x5�ɘ��c(di��n)�� 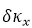 �� 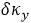 ��ɘӾ��x����b����ʹ��5x5�ɘ��c(di��n)���ش�ֱ��������һ��(g��)�y(c��)ԇ�W(w��ng)�� 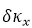 �� 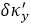 =0.5 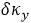 ��ɘӾ��x����c����ʹ��9x5��(g��)�ɘ��c(di��n)���x����ˮƽ�����һ��(g��)�y(c��)ԇ�W(w��ng)�� 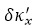 =0.5 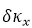 �� 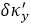 ��ɘӾ��x������b���ͣ�c���еČ�(sh��)���c(di��n)���ڣ�a���ij�ʼ�W(w��ng)���г��F(xi��n)�Ĺ�ͬ�IJɘ��c(di��n)λ�ã������ĈA�h(hu��n)�c��ʼ�W(w��ng)���в�һ�ӵIJɘ��c(di��n)��
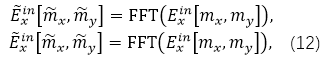
���н��V���еľ���W(w��ng)���x�� 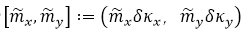 ������ 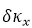 �� 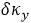 ��Kx��Ky�IJɘӾ��x������FFTӋ(j��)��ĽY(ji��)�����ڃɂ�(g��)���еIJɘ��c(di��n)��һ�ӵģ�����҂��� 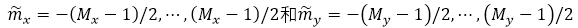 ��
����(l��i)����ݔ����V����ϵ��(sh��)��ꇣ�Ȼ���҂����ԫ@��ݔ�����V��(ch��ng)�����磬��(du��)����
���V  �IJɘ�ͨ�^(gu��)�����~׃�Q�P(gu��n)ϵ�Ԅ�(d��ng)�_����Ȼ����  �IJɘӛ](m��i)�б�Ҫ�M(j��n)�д_������?y��n)�����������ϵ�?sh��)��ݔ����V֮�g���c(di��n)�ˡ��@��(g��)��(w��n)�}���ڵ��IJ��ֵİ������M(j��n)��������f(shu��)����
һ���(l��i)�f(shu��)���ɘӾ��x 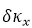 �� 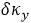 �͎��� 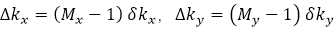 ����M(j��n)���m��(d��ng)�{(di��o)���Դ_�����_�IJɘӡ����҂�����r�У����̣�13���е��\(y��n)��](m��i)�и�׃�V��������ˣ��҂��H�Hֻ��Ҫ�ҵ����m�IJɘӾ��x���ɡ��ˆ�(w��n)�}���](m��i)�н����⣬��?y��n)�ϵ�?sh��)���T����R��ͨ�^(gu��)�f�wS��ꇷ�����(sh��)ֵ�ϫ@�õġ��_��  �ɘӵ�Ψһ�����nj�(sh��)�Д�(sh��)ֵ�y(c��)ԇ��
�҂�?c��)ڽ��V���xһ��(g��)�y(c��)ԇ�ɘӾW(w��ng)������3��b������3��c����ʾ���y(c��)ԇ�W(w��ng)���x�� 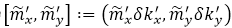 ,���� 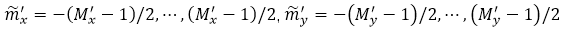 ��ָ��(sh��)�����˲���׃���V������Ҫ�� 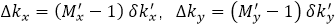 ���c��ʼ�W(w��ng)����ȣ���Ҳ��Ҫ�M(j��n)�м�(x��)�����@��ζ��  ��
һ���棬�҂���һ�N��(y��n)֔(j��n)?sh��)ķ�ʽ�?l��i)Ӌ(j��)��y(c��)ԇ�W(w��ng)���ϵ�ݔ���M����V����������ݔ��M����V�����ĺ��m�ɘӣ�����(j��)��Ҫ�����M(j��n)�в�ֵ�����磬�ڜy(c��)ԇ�W(w��ng)���ϣ��҂��@��
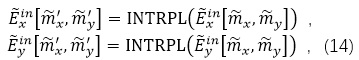
����“INTRPL”�������ǔ�(sh��)ֵ��ֵ�\(y��n)�㡣������һ��(g��)������(x��)�ľW(w��ng)���χ�(y��n)��ث@��ݔ���(ch��ng)���緽�̣�14���У��҂����Dz��û���FFT��Sinc��ֵ���������������뵽���̣�13���У����ԇ�(y��n)��ث@��ݔ���M����V��
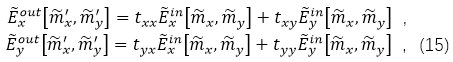
��һ���棬ͨ�^(gu��)��(du��) 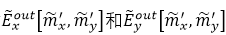 �IJ�ֵ���҂�Ҳ���ԫ@�Üy(c��)ԇ�W(w��ng)���ϵ�ݔ���M����V����������ֵ�Y(ji��)����ʾ�� 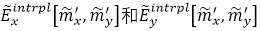 ���҂������^(gu��)��������
ֵ�Ï�(qi��ng)�{(di��o)���ǣ��ڷ��̣�16���Пo(w��)����ʹ�Ç�(y��n)���Sinc��ֵ����?y��n)��@Щ�Y(ji��)���H�H�����u(p��ng)��һ����r�����@ƪ�����У��҂�ʹ�����β�ֵ������IJ�ֵ�](m��i)��Ҫ�o�����_��ݔ��ֵ����ˣ��ڷ��̣�16������߅���҂���(du��)��Щ��ʹ���Ϙ�(bi��o)“intrpl”����һ�����҂����x
�����ֵ�Y(ji��)���͇�(y��n)��Y(ji��)��֮�g������(du��)ƫ�ֻҪ  �ڳ�ʼ�W(w��ng)���ϵIJɘӝM���ο�˹��-���r(n��ng)�ɘӶ��������������IJ�ֵ�Y(ji��)���Ͳ���(hu��)��(du��)��(y��n)��IJ�ֵ�������F(xi��n)��һ��(g��)���ƫ����@�N��r�£�����(j��)���x�IJ�ֵ�������ɷN�Y(ji��)����ƫ�(y��ng)ԓ�ڔ�(sh��)ֵ�`�(j��)�Σ���σ_0��ʾ��ʹ��������(bi��o)��(zh��n)��ͨ�^(gu��)һ�����ĜpС�ɘ��g����(l��i)�y(c��)ԇ��(ch��ng)�ɘӣ�ֱ��σ<σ_0��
���ϵĜy(c��)ԇ�^(gu��)�̌�(du��)��(y��ng)��һ��(g��)ѭ�h(hu��n)����ÿ��(g��)�y(c��)ԇѭ�h(hu��n)�ж���(hu��)��(zh��)�з��̣�14������17����Ӌ(j��)�㡣������ÿ��(g��)�y(c��)ԇѭ�h(hu��n)�г�ֵ�ʹ�Üy(c��)ԇ��(sh��)��(j��)���緽�̣�15���еĽY(ji��)�����҂�����ʹ�ÈD3��b����3��c���еĜy(c��)ԇ�W(w��ng)���@��Ҏ(gu��)�t�Ĝy(c��)ԇ�W(w��ng)���x��
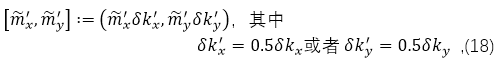
��(du��)ÿ��(g��)ѭ�h(hu��n)��(n��i)����Ҫ��(du��)��ǰ�IJɘӾ��x�p�롣ʹ���@��(g��)�y(c��)ԇ�W(w��ng)��������º�̎����(d��ng)Ӌ(j��)�� 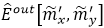 �r(sh��)���H�H��ҪӋ(j��)����Щ�ڿ��ĈAȦλ��̎��ֵ������(sh��)���c(di��n)λ��̎��ֵ��֮ǰ�Ĝy(c��)ԇѭ�h(hu��n)���ѽ�(j��ng)Ӌ(j��)���^(gu��)�ˣ������@Щֵ��(ji��n)�ε��M(j��n)�Ђ�ݔ���ɡ����@�N��ʽ�£��@Щ���ڜy(c��)ԇĿ�����M(j��n)�Ї�(y��n)��Ӌ(j��)���ֵ����(hu��)���G��������(hu��)������һ��ѭ�h(hu��n)�е���ʼ�c(di��n)������ʹ�á���ˣ���һ��(g��)������Ӌ(j��)��������(zh��)�е��LJ�(y��n)���Ӌ(j��)�㣬�Ķ��(y��n)�C���m�IJɘӣ������@ЩӋ(j��)���ֵ�܉���Ч�����ژ�(g��u)����Kݔ����(ch��ng)���҂�������ķ������Y(ji��)���㷨1�С�
�㷨1��ͨ�^(gu��)���m�IJɘӿ��Ɓ�(l��i)�M(j��n)��ݔ�����VӋ(j��)��Ĕ�(sh��)ֵ����
1)�ڳ�ʼ�W(w��ng)���(y��n)���Ӌ(j��)�� 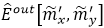
2)��ʼ������(du��)�`��ֵσ=+∞
3)�Д�σ>σ_0�� ⊳������棬�t�ɘӲ����m
4)��Kx������Ky�����ȷֲɘӾ��x
5)��(y��ng)���µIJɘӾ��x���x�y(c��)ԇ�W(w��ng)�� 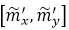
6)�ڜy(c��)ԇ�W(w��ng)���Ќ�(du��)ݔ����V��ֵ������(j��)���̣�14���@�� 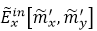
7)����(j��)���̣�15�����ڜy(c��)ԇ�W(w��ng)���χ�(y��n)���Ӌ(j��)��ݔ�����V 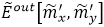
8)����(j��)���̣�16����ͨ�^(gu��)��ֵ�@�� 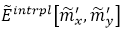
9)����(j��)���̣�17����Ӌ(j��)���`��σ
10)���σ>σ_(0 ) 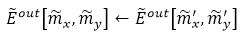 ���t⊳��Ŀǰ��ݔ����(ch��ng)�O(sh��)�Þ���һ��ѭ�h(hu��n)����ʼ�c(di��n)
11)���� 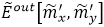
������Ч��̎���nj�(du��)�Q(ch��ng)��r�����磬������x�����y�����в�ͬ�İl(f��)ɢ�ǣ��㷨1�еĜy(c��)ԇ��Ҫ������ɂ�(g��)�����M(j��n)�С��_(k��i)ʼ������x��������ģ����҂�����r�У��҂�����y�����_(k��i)ʼ�y(c��)ԇ�ġ�
4.ʾ��
��VirtualLab Fusion[42]ܛ���У��҂���������(ji��)��������㷨��(sh��)�F(xi��n)��“�ɾ���Ԫ��”�ľ��̽����С��@��(g��)Ԫ�������cVirtualLab Fusion��������������W(xu��)���漼�g(sh��)�M(j��n)��(li��n)�Ϸ��档����(l��i)���҂�չʾ���Ă�(g��)������ǰ�ɂ�(g��)��Ҫ�P(gu��n)עԪ����������һ�N��(y��n)��Ĕ�(sh��)ֵ��ʽ�z����㷨����ɂ�(g��)�����У�Ԫ�������ڹ�W(xu��)ϵ�y(t��ng)�У����磬���㷨�c�������漼�g(sh��)һ��ʹ�á�
���M(j��n)�댍(sh��)�H�İ���֮ǰ���O(sh��)�÷��̣�17���еĵ����Kֹ��(bi��o)��(zh��n)σ_0����Ҫ����(du��)���ڴ�������ʹ�õ����β�ֵ���҂��A(y��)�șz��������һ����r�µı��F(xi��n)�����҂��Ĕ�(sh��)ֵ�h(hu��n)�����ҵ���һ��(g��)0.01�Ļ���(zh��n)ֵ��
A.����ͬ�Ԙ�(bi��o)��(zh��n)��
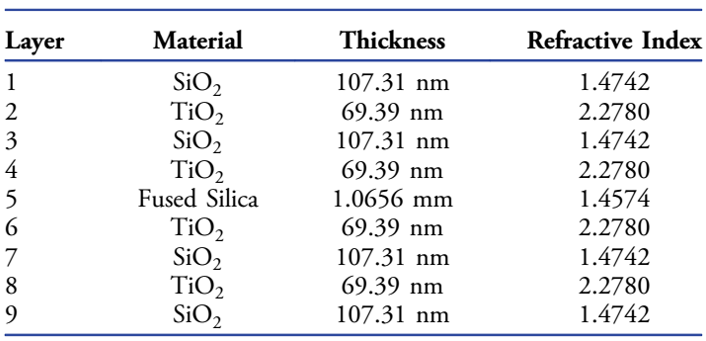
��һ��(g��)����ģ�M��һ��(g��)����ƫ���˹������(j��ng)�^(gu��)һ��(g��)��(bi��o)��(zh��n)�ߵĂ�ݔ��ͨ�^(gu��)�@��(g��)�������҂��������ָ��������(ji��)�����f(shu��)�IJɘӆ�(w��n)�}���������㷨1�Ĺ���ԭ������(bi��o)��(zh��n)��������ʯӢ�Ƴɣ��ɂ�(c��)�ж��ӱ�Ĥ����D4��ʾ���P(gu��n)�ژ�(bi��o)��(zh��n)�ߵĹ�W(xu��)����(sh��)�ͽY(ji��)��(g��u)�ĸ�����Ϣ��Ո(q��ng)Ҋ(ji��n)��1��ݔ���(ch��ng)�鲨�L(zh��ng)633nm��x����ƫ��ĸ�˹����������Ԫ����ݔ��ƽ�涨�x��E_⊥^in,�������돽�飨2um��2um�����ڽ�(j��ng)�^(gu��)�����~׃�Q���҂��@������V��ͬ�Ӿ��и�˹݆������D5��ʾ�����շ��̣�10���еIJ����������У�ݔ����V����������߷�����ϵ��(sh��)���҂�?n��i)������������ӣ����Ҍ?du��)�ھ���ƫ��ݔ���(ch��ng)���҂�ʹ��t_xx��t_yx����E ̃_x^in���ԫ@��ݔ�����V������
�D4.������ʯӢ�Ƴɣ��ɂ�(c��)�ж���Ĥ�Ę�(bi��o)��(zh��n)�ߡ���Y(ji��)��(g��u)��W(xu��)����(sh��)���1����ʾ��
��1 ��(bi��o)��(zh��n)�ߵĽY(ji��)��(g��u)��W(xu��)����(sh��)
�D5 .��a��ݔ���˹��(ch��ng)�������������b����(du��)��(y��ng)�Ľ��V����������ݔ����(ch��ng)����x����ľ���ƫ��⣬��˃H�@ʾEx������
�������(ji��)����ָ�����˷e  �IJɘӲ����Ԅ�(d��ng)�õ����C���˰����Ќ��@ʾԓ�F(xi��n)��(bi��o)��(zh��n)���������l���x���ܣ��l�V����l�ʣ����õ��V����ʹ�á����҂��İ����У����l���x����Խ�ጞ�ϵ��(sh��) txx�� tyx��һ�N��ʽ�{(di��o)��ݔ����V����ʹ�ض��Ľ��l�ʼӏ�(qi��ng)�������Ĝp�����@�N�{(di��o)�ƿ��Գ��F(xi��n)��һ�N�dz�����(x��)���l��ˮƽ�ϡ���ˣ���Ҫʹ�ø�����(x��)�IJɘ�����ݔ�����V�н����@��һ��(g��)����(x��)���{(di��o)�ơ����˫@����Ҫ�IJɘ��g�࣬�҂���ѭ�㷨1���D6���@ʾ�˲��ֽY(ji��)����
ͨ�^(gu��)�D6�ͱ�2���҂�����(j��)�㷨1�еIJ��E�����˹������̣����£�
��һ�����ĈD6��a������ʾ��ݔ����V�_(k��i)ʼ��Ӌ(j��)�����(g��)ϵ��(sh��)������Ԫ����������ɳ�ʼ����ݔ�����V��
�ڶ�������ʼ������(du��)ƫ��σ=+∞��
���������_(k��i)ʼ�y(c��)ԇѭ�h(hu��n)��
����&�岽�����ɘӾ��x��κ_x����κ_y����p�룬�Զ��x�y(c��)ԇ�W(w��ng)�� 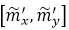 ����(du��)��(y��ng)�IJɘ��c(di��n)���2����ʾ��
����������(du��)ݔ����V�ڜy(c��)ԇ�W(w��ng)���ϲ�ֵ��
���߲����ڜy(c��)ԇ�W(w��ng)���χ�(y��n)���Ӌ(j��)��ݔ�����V 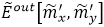 ���ڴ����У���(du��)��(y��ng)�D6��e����
�ڰ˲�����(zh��)�в�ֵ�ԫ@�� 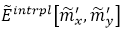 ���ڴ����Ќ�(du��)��(y��ng)�D6��b��-6��d����
�ھŲ������^��(y��n)�����Ͳ�ֵ�Y(ji��)������Ӌ(j��)������(du��)�`�
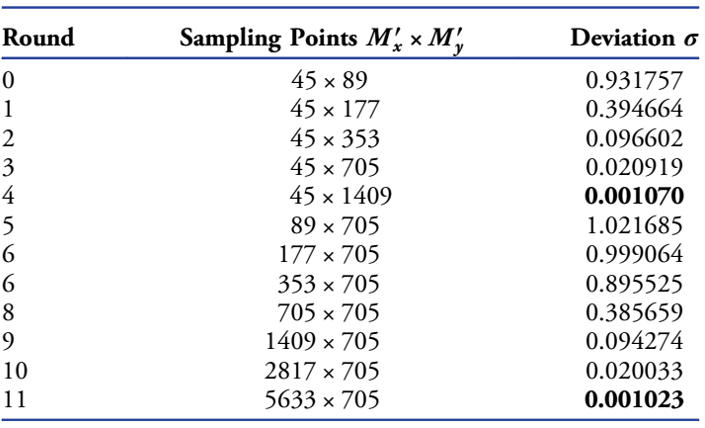
��ʮ������(du��)���^��IJ�ֵ�Y(ji��)������6��b����6��c������2�е�0-3�У���Y(ji��)����σ>σ_0����(y��n)��ĽY(ji��)�� 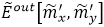 ����(hu��)���f�o��һ��(g��)ѭ�h(hu��n)������ݔ�룻��t�����خ�(d��ng)ǰ�ĽY(ji��)����
�D6.�㷨1�в�ͬ���E�r(sh��)��κ_x�����һ�S��ȡ�Y(ji��)������a��ݔ����V�������b��-��d�����ڜy(c��)ԇѭ�h(hu��n)�еIJ�ֵ���V����Լ���e��������ѭ�h(hu��n)�Ї�(y��n)���Ӌ(j��)��ݔ�����V�����е��ӈD�е�ֵ���s�ŵ���ͬ�ķ�����(n��i)��
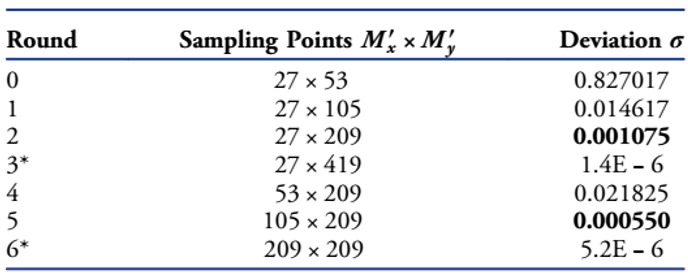
�ı�2���҂�Ҳ���Կ����y(c��)ԇ��������y����֮������x�����(zh��)�еģ��������(ji��)��������ᵽ�ġ��ĵ�0݆����4݆�y(c��)ԇ���ɘӾ��xδκx���](m��i)�и�׃����˲ɘ��c(di��n)Mx^�����ֲ�׃���ڵ���݆�y(c��)ԇ��σ<σ0����y����Ĝy(c��)ԇ�Kֹ����ζ����(ch��ng)��(sh��)��(j��)�ѽ�(j��ng)���ԏ���ǰһ݆�ĽY(ji��)���л֏�(f��)����ˣ���y����IJɘ��c(di��n)��(sh��)��705���ڵ���݆���~���704��(g��)��(sh��)��(j��)�H�H�����ڜy(c��)ԇĿ�ģ���(du��)��K��ݔ�����](m��i)��ؕ�I(xi��n)��Ȼ����һ�N�(l��i)�Ƶķ�ʽ��x�����_(k��i)ʼ�y(c��)ԇ���ڵ�11݆�Kֹ��ͬ�ӣ���(ch��ng)��(sh��)��(j��)���ԏ���ǰһ݆�ĽY(ji��)���л֏�(f��)����ˣ���Kݔ���IJɘ��c(di��n)��(sh��)�̶���2817x705���ڱ�2�Ĝy(c��)ԇ݆�У������Ŀ��IJɘ��c(di��n)��(sh��)��5633x705+45x704����(sh��)��(j��)45x704��(l��i)������y��������y(c��)ԇ݆���ٴΏ�(qi��ng)�{(di��o)һ�£������ڽ��V���M(j��n)�к��m�IJɘӣ��б�Ҫ������˴�IJɘ��c(di��n)��(sh��)�����ң�������x�������y�������һ݆�y(c��)ԇ�����ڜy(c��)ԇĿ�Ķ����Ї�(y��n)��Ӌ(j��)���ֵ�����ژ�(g��u)����Kݔ����(ch��ng)��
��2 Etalonģ�M��ÿ��(g��)�y(c��)ԇ݆���еIJɘӅ���(sh��)���`��
�����е�ģ�M��ʹ�õ���һ�_(t��i)Intel Core i7-4910MQ̎����,2.9GHz��32Gb�����(n��i)�����X����2�����@ʾ��ʾ������Ŀ���Ӌ(j��)��r(sh��)�g��118s��ע��Ӌ(j��)��r(sh��)�g���IJ����ǻ���S���Ӌ(j��)���ϣ�������E�ĸ����~��׃�Q�H���˼s0.5s��
�ı�2��Ҳ���Կ�����x�������y����Ĝy(c��)ԇ݆�Δ�(sh��)Ҳ��һ�ӣ����ɂ�(g��)��������IJɘ��g�ͬ����ˣ��҂�?c��)��㷨�и��A����ÿ��(g��)����քe��(zh��)�вɘӜy(c��)ԇ��
ͨ�^(gu��)�@��(g��)�㷨���҂��@���˘�(bi��o)��(zh��n)�ߵ��^(gu��)��(ch��ng)����D7��ʾ�����ˈD7�����(ch��ng)�ijߴ��h(yu��n)���ڈD5�е�ݔ���(ch��ng)������ݔ����(ch��ng)���� 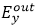 Ҳֵ��ע�⣬�M�������Ҫ�h(yu��n)С�� 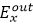 ��Ex��Ey֮�g���F(xi��n)��ƫ��?d��ng)_������ϵ��(sh��)���T����R�ķnj�(du��)����ʽ��ɵġ��� 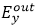 ������ֲ��У�߀���Կ�������(x��)��ͬ�ĈA���@�����ژ�(bi��o)��(zh��n)�߶��ӽY(ji��)��(g��u)�аl(f��)���Ķ��ط�����ɵġ�
�D7.�������λ�o���Ę�(bi��o)��(zh��n)��ݔ����(ch��ng)�������������a����|E_x^out |����b����|E_y^out |
B.���S���w��
�҂��ķ�����(du��)����ͬ�Խ��|(zh��)�Ӻ����Խ��|(zh��)�Ӷ�ͬ���m�á����@��(g��)�����У��҂���ʾ�˾۹����x��ԭ������������ھ��_�Ĝy(c��)�����S���w�Ĺ��S�Aб�Ƕ�[43]����(d��ng)ʹ�Õ�(hu��)�ۆ�ɫ����������ƫ�����g�ľ��w�r(sh��)�����ɮa(ch��n)���۹���档�D8��չʾ�˾۹����x�ĺ�(ji��n)Ҫԭ�������҂���ģ�M�У���Դ��һ��(g��)Ex����ƫ���L(zh��ng)��633nm��NA=0.25�����沨���ھ��w��ǰ20mm����Դ��ݔ���(ch��ng) 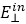 ���f�����w���ǰ���棬������ݔ����(ch��ng)�������������@��(g��)�ӹ�(ji��)�У��҂��](m��i)��ӑՓ���w��Ԫ���ⲿ�^(q��)��Ă������E��
�D8.ʹ�þ۹����x�y(c��)�����S�ĽǶȡ�ƫ��ƬP1��x����ƫ��ƬP2��y�����S��ʾ��“o.a”��
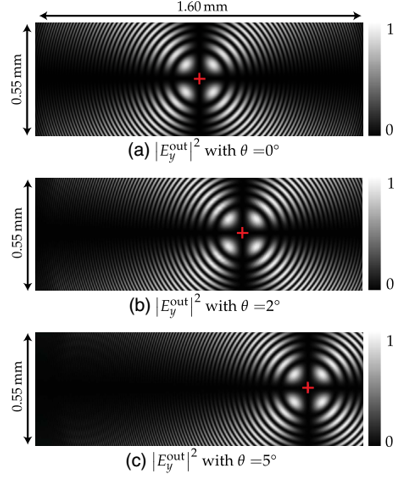
�҂�ʹ�þ۹����x���y(c��)ԇ��һ��(g��)6mm�������Һ���壬����S�cz�S��θ�ǡ�����n_e=1.7��n_0=1.5[43]���O(sh��)θ=0°��2°�Լ�5°���҂��^���˾��w���y�����ݔ����(ch��ng)����D9��ʾ����(d��ng)θ=0°�����w�Ĺ��S��ֱ�ھ��w����棬ͬ�ĭh(hu��n)��ԭ�c(di��n)λ�����ģ���D9��a����ʾ����(d��ng)θ≠0°�r(sh��)��������еĈD9��b����
�D9��c����ͬ�ĭh(hu��n)��ԭ�c(di��n)����(y��ng)�İl(f��)���˙M��ƫ�ơ��҂�?c��)�ģ�M�Ы@�õ�ֵ�c�����īI(xi��n)[43]�з����ĽY(ji��)��һ�¡�
�D9.ᘌ�(du��)��ͬ��θֵ���ھ��w�������ݔ����(ch��ng)�ֲ������ƽ������ʹ����y�����ƫ��ƬP2����ݔ����(ch��ng)����˃H�@ʾ��E_y�������tɫ��ʮ�֘�(bi��o)����ͬ�ĈA�h(hu��n)��ԭ�c(di��n)���飨0��0������210um��0���Լ���525um��0�����քe��(du��)��(y��ng)�ӈD��a������b���ͣ�c����
���˫@�ÈD9�е����(ch��ng)���㷨1�ٴα����ڴ_���ɘӾ��x�����������ԣ���3�нo����θ=5°�r(sh��)�����вɘӾ��x�Ĕ�(sh��)ֵ�y(c��)ԇ�ļ�(x��)��(ji��)��
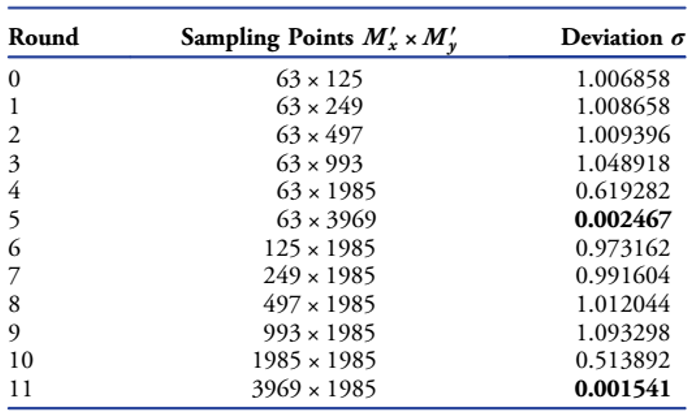
�ڱ�3���@ʾ�Ĝy(c��)ԇ݆���У�������3969x1985+63x1984��(g��)�ɘ��c(di��n)����(du��)��ÿ��(g��)�ɘ��c(di��n)��Ӌ(j��)���˸�����S��ꇣ��ĕr(sh��)416s��
��3.���S��5°�Ć��S���w����ÿ��(g��)�y(c��)ԇ݆���еIJɘӾ��x��ƫ��
C.�Aб�ĸ����Ծ��w��ϵ�y(t��ng)
���һ��(ji��)�������҂��_(k��i)�l(f��)���㷨��ϵ�y(t��ng)��ģ��һ���֡����@��(g��)�����У��҂�ģ�M��һ��(g��)��������ʯ���w��Ĺ�W(xu��)ϵ�y(t��ng)���о�ƫ���D(zhu��n)�Q�Լ��u��������[44]����D10��ʾ����?y��n)���ᘌ?du��)����(g��)ϵ�y(t��ng)�M(j��n)�н�ģ�������̎���^(gu��)��ʹ���ˎN��ͬ�Ĉ�(ch��ng)�E����[27]��ƫ��Ƭʹ�í�˹������ӣ��R����(d��ng)���������R�����Aб����ʯ�����Ĺ��(ch��ng)��ݔʹ�Å����īI(xi��n)[33]�еļ��g(sh��)������ʯ���еĹ��(ch��ng)��ݔ�tʹ���˴����еķ�����
����(j��)�����īI(xi��n)[44]���o���˷���ʯ���w�����ʣ�����

����λ��λ���ס�
�D10.�����Aб���w���ϵ�y(t��ng)�����w����Ϟ鷽��ʯ����Ȟ�6mm�����S�ڈD����“o.a.”��ʾ����ֱ�ھ��w����档ƫ��ƬP1����������x�����ƫ��⣬��ƫ��ƬP2���ڷ������RL1��L2�����30mm��
�������҂���α=0°�_(k��i)ʼ����ϵ�y(t��ng)�Ўׂ�(g��)λ�õĈ�(ch��ng)�ֲ���D11��ʾ����ƫ��ƬP1ǰ��ݔ���(ch��ng)�鲨�L(zh��ng)633nm��x�����y���������돽1.5mm�ĸ�˹��������(j��ng)�^(gu��)ƫ��ƬP1֮�@����һ��(g��)��x����ľ���ƫ���(ch��ng)���RL1��ľ۽���(ch��ng)�Ƿ���ʯ���w���ݔ���(ch��ng)������(j��)�㷨1���҂��@���˾��w�������ݔ����(ch��ng)����D11��a����11��b���������ƫ��ƬP2֮���ƽ���ϣ��҂��@����ϵ�y(t��ng)��ݔ����(ch��ng)����D11��c����11��d����ʾ��
�D11.�D10�з���ʯ���w�弰P2ƫ��Ƭ��Ĉ�(ch��ng)�ֲ������ƽ������������α=0°��
�҂���(l��i)�м�(x��)���^��һ�D11����չ�F(xi��n)�ĽY(ji��)������(sh��)ֵ�y(c��)ԇ��(x��)��(ji��)�ڱ�4�нo�����c4A���ֵ���r���ƣ�����T����R�ķnj�(du��)�Ǿ���ʽ����x����ľ���ƫ��ݔ���(ch��ng)��ݔ����(ch��ng)������һ��(g��)����yƫ���������І��S���w���ƫ��?d��ng)_����(du��)����(qi��ng)��E(x )≈E(y ),���ژ�(bi��o)��(zh��n)�ߵ������У�E(x )��E(y )�ı��������1000��1����D7��a����7��b�����@�����ڷ���ʯ���w���p�������|(zh��)����(d��o)��E(x )��E(y )����֮�g����һ��(g��)��(qi��ng)����ϡ�
��4 1.5mm��˹�������䵽���S���w�壬��ÿ��(g��)�y(c��)ԇ݆���еIJɘӾ��x��ƫ��
P2��Ĉ�(ch��ng)����D11��e����11��f����ʾ���c�����īI(xi��n)[44]�еĜy(c��)���Y(ji��)���Ǻϵĺܺá��������p����������ĘO�Y(ji��)��(g��u)���҂�ͬ��Ҳ�����˯B�������ϵ�ͬ�ĈA�h(hu��n)�Y(ji��)��(g��u)���c�D11�ķ����(l��i)�ƣ��@Щ����(x��)�Y(ji��)��(g��u)�����ڰ��(n��i)�Ķ��ط�����ɵġ������څ����īI(xi��n)[44]�еĈD4�п���ͬ�ӵ�Ӱ푣��M�܌�(sh��)�(y��n)�y(c��)���Č�(du��)�ȶ��^�͡�
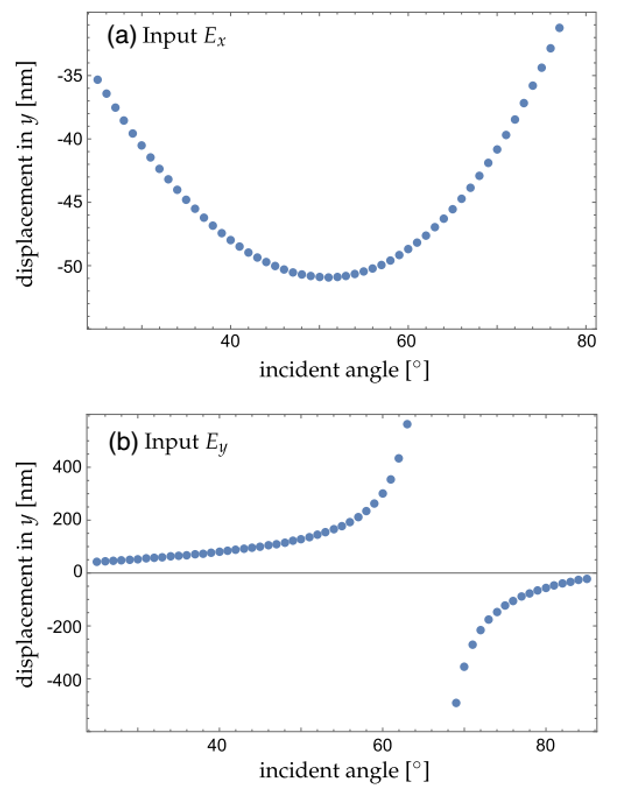
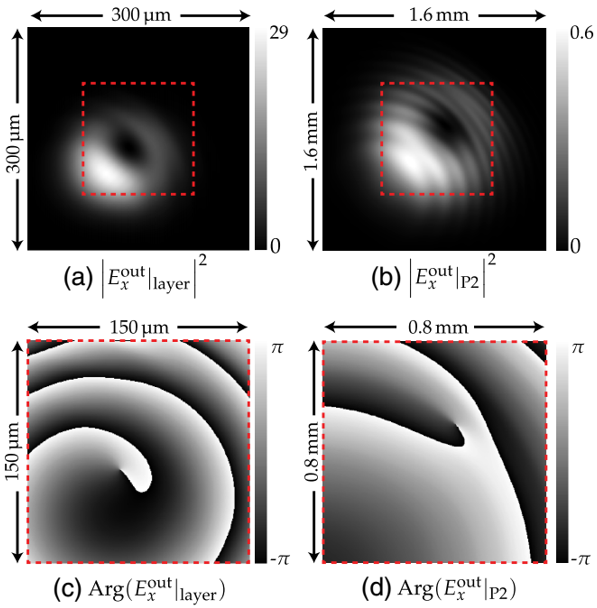
��һ�����煢���īI(xi��n)[44]����չʾ���҂������w�Aбһ���ĽǶ�α����ݔ���˹�����O(sh��)�Þ�0.5mm�������ɆΘO��u����ģ�M�У��҂�ʹ��[33]�еķ���̎����ƽ�а�֮�g�Ă�ݔ��ͨ�^(gu��)�@�N��ʽ�����ԫ@�ÃAб���w������ݔ���(ch��ng)���҃Aб������ݔ����(ch��ng)�����^�m(x��)��ݔ����һ��(g��)Ԫ����ģ�M�Y(ji��)����D12��13��ʾ����(d��ng)α=1.2°�r(sh��)�������ڱ�5�Ы@�òɘӾ��x�Ĕ�(sh��)ֵ�y(c��)ԇ��(x��)��(ji��)�����Կ�������x�����y�����ƫ��σ�քe��݆��2��5�НM��ֹͣ�Г�(j��)���҂��ɂ�(g��)�����^�m(x��)��ǰ����һ�Σ���(bi��o)ӛ��*���ԫ@��һ��(g��)�^(gu��)�ɘӣ��Ԟ��˸��õ��c֮��ķ�ƽ��ƽ���g�Ă�����Y(ji��)��[33]���@֮�g�Ă���ͨ����Ҫ�^(gu��)�ɘ����Ӟ�2.
�D12.��(d��ng)α=0.8°�r(sh��)������ʯ���w���ƫ��ƬP2֮���ݔ����(ch��ng)�����ƽ����
�D12��13�ٴ��c�����īI(xi��n)[44]�еĽY(ji��)��һ�¡��c֮ǰ����α=0°�r(sh��)����r�(l��i)�ƣ���u���Y(ji��)��(g��u)���ɷ���ʯ���w���p����a(ch��n)���ġ���D13��c����13��d����ʾ��ͬ��Ҳ���Կ�����λ�e(cu��)λ����Ĺ�u�������˜u�����D13��b����߀���Կ����h(hu��n)�εľ���(x��)�Y(ji��)��(g��u)���@�����ھ��w���(n��i)�Ķ��ط�����ɵġ�
����5�еĔ�(sh��)��(j��)�y(c��)ԇ�c֮ǰ���M(j��n)�б��^���҂����Կ���һ��(g��)������Ք����e����x����Ĝy(c��)ԇ��������5�е����Мy(c��)ԇѭ�h(hu��n)����(j��ng)�^(gu��)�Aб�ķ���ʯ���w��Ă�ݔ�Hʹ���˴�s4s��Ӌ(j��)��r(sh��)�g������ˣ�������(g��)ϵ�y(t��ng)��ģ�M�������R����s��30s�ĕr(sh��)�g�����ڷ���ʯ���@y�S�Aб1.2°�����w��������酢�����t��(du��)��(y��ng)��һ��(g��)�p�ăAб�����(ch��ng)������(j��)�����~׃�Qƫ����Փ����y����ăAб����(d��o)�½��V�ش˷�����һ��(g��)ƫ�ơ���ˣ����(ch��ng)�Ľ��Vͬ�Ӵ�����x�����y����IJ�ͬ�{(di��o)�ơ�
�D13.��(d��ng)α=1.2°�r(sh��)������ʯ���w���ƫ��ƬP2���ݔ����(ch��ng)�����У�a���ͣ�b�������ƽ���ķֲ�����c���ͣ�d������λ�ֲ�
��5 0.5mm��˹�������䵽�Aб���w��r(sh��)��ÿ݆�y(c��)ԇ�еIJɘӅ���(sh��)��ƫ��
D.�ڿ՚�-���S����ķ���
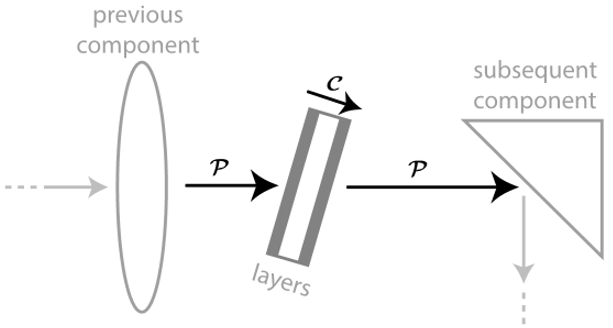
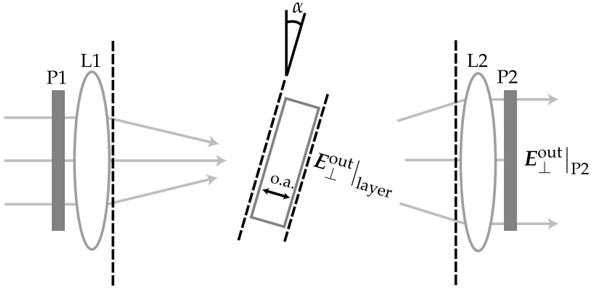
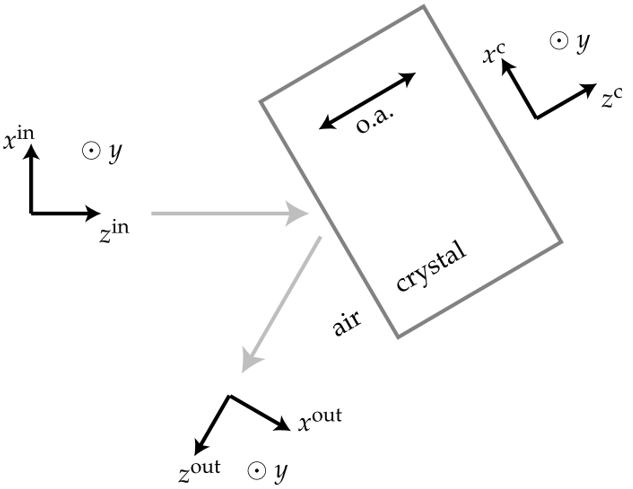
��(du��)�ڷ�����r��ͬ�������(l��i)�����㷨�е�����r�ķ����M(j��n)��̎�����҂���������չʾ���҂��x���īI(xi��n)[45]�Ĺ��������՚�-���S���w����l(f��)������������Ч��(y��ng)����(l��i)����һ��(g��)���ӡ�ϵ�y(t��ng)ԭ��D��D14��ʾ�����������P(gu��n)�{������(j��)ƫ�ƿ���ͨ�^(gu��)�z�鷴���(ch��ng)�����ā�(l��i)�M(j��n)�Мy(c��)����
�D14.�ڿ՚�-���S���w����ķ��䡣���wԪ��ʹ�� 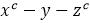 ����(bi��o)ϵ�y(t��ng)��(l��i)��ʾ������S��o.a.���� 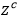 ����ݔ��ͷ����(ch��ng)���� 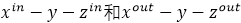 �нo��
���҂���ģ�M�У�ʹ���˲��L(zh��ng)��632.8nm�ľ���ƫ���˹��(ch��ng)����ݔ���(ch��ng)���ڴ˲��L(zh��ng)�£���(du��)��o���e�⣬LiNbO3���w��Ʒ�������ʷքe��n0=2.232��ne=2.156�����īI(xi��n)[45]�в��](m��i)�нo��ݔ�����(ch��ng)�Ĺ����ߴ磬�҂������O(sh��)�Þ�20um�����ڷ����(ch��ng)�ęM��ƫ�����ɿ��g�l�����еľֲ�������λ�Q���ģ���˲���׃�����ߴ�Ĵ�С��
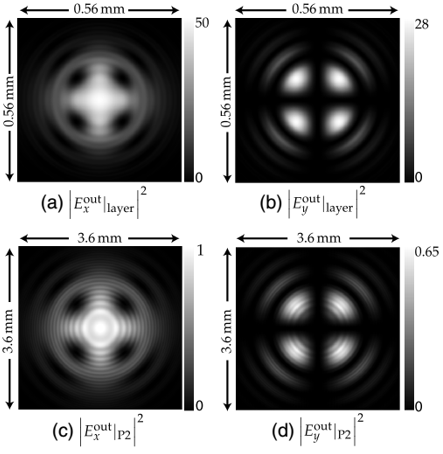
�����о���Ч��(y��ng)������ʸ����(ch��ng)ͶӰ�ڈAƫ��λʸ������(bi��o)ϵ�������҂��y(c��)���������Aƫ����������ġ����⣬��(du��)Ex��Ey�ɂ�(g��)����ƫ�������(ch��ng)���҂����D(zhu��n)���wԪ�����O(ji��n)��λ���S������Ƕȵ�׃����ģ�M�Y(ji��)����D15����ʾ��
�҂�ʹ�Å���(sh��)����@�ÈD15�еĽY(ji��)������(du��)��ÿ��(g��)����Ƕȣ��҂�ʹ���҂����㷨Ӌ(j��)���˷����(ch��ng)������һ��(g��)��ĽǶȷ�����(n��i)�@ʾ�����^�õ��m��(y��ng)�ԡ�ģ�M�Y(ji��)���c[45]�еĽY(ji��)��ƥ��ĺܺá�
�D15.����Ƕ��c�҈Aƫ���������(ch��ng)�ęM��ƫ��֮�g���P(gu��n)ϵ����a��Ex�ͣ�b��Ey�քe�龀��ƫ��ݔ�롣
���Y(ji��)
�҂���ϵ�y(t��ng)����ĽǶ��о���늴ň�(ch��ng)��(j��ng)�^(gu��)����ͬ�Ի�����Ԍӽ��|(zh��)Ԫ���Ă�ݔ������SPW���������Է��̣�10������ʽ�����ĽY(ji��)�����Ԟ���m(x��)�Ĕ�(sh��)ֵ��(sh��)�F(xi��n)����(zh��n)�䡣�҂������ӑՓ���ںܶ���(sh��)�H��(w��n)�}�Е�(hu��)�����IJɘӆ�(w��n)�}�����⣬�҂������һ�N��(sh��)ֵ�y(c��)ԇ�㷨���Ը���Ч���ڽ��V��_���ɘӅ���(sh��)��ͨ�^(gu��)��(bi��o)��(zh��n)�ߵİ������҂�?c��)��?x��)���������҂����㷨�Ĺ������̣��@ʾ���҂�������һ����Ч�ԡ��˷����ѽ�(j��ng)�ɹ��ؑ�(y��ng)�õ��ˌ�(du��)���⾧�w���b���g(sh��)�еđ�(y��ng)���T��(d��o)�p����ķ���[46]��
���x
�҂����xOlga Baladron-ZoritaŮʿ��(du��)�����µ�У���Լ����ճ��Ď�����
�����īI(xi��n)
B. R. Horowitz and T. Tamir, “Lateral displacement of a light beam at a dielectric interface*,” J. Opt. Soc. Am. 61, 586–594(1971).
M. McGuirk and C. K. Carniglia, “An angular spectrum representation approach to the Goos–Hänchen shift,” J. Opt. Soc. Am. 67, 103–107(1977).
S. Kozaki and H. Sakurai, “Characteristics of a Gaussian beam at a dielectric interface,” J. Opt. Soc. Am. 68, 508–514 (1978).
C. C. Chan and T. Tamir, “Angular shift of a Gaussian beam reflected near the Brewster angle,” Opt. Lett. 10, 378–380 (1985).
F. I. Baida, D. V. Labeke, and J.-M. Vigoureux, “Numerical study of the displacement of a three-dimensional Gaussian beam transmitted at total internal reflection near-field applications,” J. Opt. Soc. Am. A17, 858–866 (2000).
S. Zhang, D. Asoubar, F. Wyrowski, and M. Kuhn, “Efficient and rigorous propagation of harmonic fields through plane interfaces,”Proc. SPIE 8429, 84290J (2012).
M. Tanaka, K. Tanaka, and O. Fukumitsu, “Transmission and reflection of a Gaussian beam at oblique incidence on a dielectric slab,” J. Opt. Soc. Am. 67, 819–825 (1977).
S. Kozaki and H. Harada, “Beam displacement of a reflected beam at an interface between an inhomogeneous medium and free space,”J. Opt. Soc. Am. 68, 1592–1596 (1978).
C. W. Hsue and T. Tamir, “Lateral displacement and distortion of beams incident upon a transmitting-layer configuration,” J. Opt.Soc. Am. A 2, 978–988 (1985).
R. P. Riesz and R. Simon, “Reflection of a Gaussian beam from a dielectric slab,” J. Opt. Soc. Am. A 2, 1809–1817 (1985).
T. Tamir, “Nonspecular phenomena in beam fields reflected by multilayered media,” J. Opt. Soc. Am. A 3, 558–565 (1986).
J. J. Stamnes and D. Jiang, “Focusing of electromagnetic waves into a uniaxial crystal,” Opt. Commun. 150, 251–262 (1998).
J. J. Stamnes and V. Dhayalan, “Transmission of a two-dimensional Gaussian beam into a uniaxial crystal,” J. Opt. Soc. Am. A 18,1662–1669 (2001).
J. J. Stamnes and V. Dhayalan, “Double refraction of a Gaussian beam into a uniaxial crystal,” J. Opt. Soc. Am. A 29, 486–497(2012).
L. I. Perez, “Reflection and non-specular effects of 2d Gaussian beams in interfaces between isotropic and uniaxial anisotropic media,” J. Mod. Opt. 47, 1645–1658 (2000).
L. I. Perez, “Nonspecular transverse effects of polarized and unpolarized symmetric beams in isotropic-uniaxial interfaces,” J. Opt. Soc.Am. A 20, 741–752 (2003).
S. Stallinga, “Axial birefringence in high-numerical-aperture optical systems and the light distribution close to focus,” J. Opt. Soc. Am.A 18, 2846–2859 (2001).
S. Stallinga, “Light distribution close to focus in biaxially birefringent media,” J. Opt. Soc. Am. A 21, 1785–1798 (2004).
M. Jain, J. Lotsberg, J. Stamnes, and Ø. Frette, “Effects of aperture size on focusing of electromagnetic waves into a biaxial crystal,” Opt.Commun. 266, 438–447 (2006).
M. Jain, J. K. Lotsberg, J. J. Stamnes, Ø. Frette, D. Velauthapillai, D.Jiang, and X. Zhao, “Numerical and experimental results for focusing of three-dimensional electromagnetic waves into uniaxial crystals,”J. Opt. Soc. Am. A 26, 691–698 (2009).
S. Zhang and F. Wyrowski, “Simulations of general electromagnetic fields propagation through optically anisotropic media,” Proc. SPIE 9630, 96300A (2015).
D. Asoubar, S. Zhang, and F. Wyrowski, “Simulation of birefringenceeffects on the dominant transversal laser resonator mode caused by anisotropic crystals,” Opt. Express 23, 13848–13865(2015).
G. D. Landry and T. A. Maldonado, “Gaussian beam transmission and reflection from a general anisotropic multilayer structure,” Appl. Opt.35, 5870–5879 (1996).
V. Dhayalan and J. J. Stamnes, “Focusing of electromagnetic waves into a dielectric slab, I: exact and asymptotic results,” Pure Appl. Opt.7, 33–52 (1998).
V. Dhayalan and J. Stamnes, “Focusing of electromagnetic waves into a dielectric slab, II: numerical results,” J. Eur. Opt. Soc. 6,11036 (2011).
A. Turpin, Y. V. Loiko, T. K. Kalkandjiev, and J. Mompart, “Light propagation in biaxial crystals,” J. Opt. 17, 065603 (2015).
F. Wyrowski and M. Kuhn, “Introduction to field tracing,” J. Mod. Opt.58, 449–466 (2011).
D. Asoubar, S. Zhang, F. Wyrowski, and M. Kuhn, “Parabasal field decomposition and its application to non-paraxial propagation,”Opt. Express 20, 23502–23517 (2012).
D. Asoubar, S. Zhang, F. Wyrowski, and M. Kuhn, “Efficient semianalytical propagation techniques for electromagnetic fields,”J. Opt. Soc. Am. A 31, 591–602 (2014).
H. Zhong, S. Zhang, and F. Wyrowski, “Parabasal thin-element approximation approach for the analysis of microstructured interfaces and freeform surfaces,” J. Opt. Soc. Am. A 32, 124–129 (2015).
F. Wyrowski, H. Zhong, S. Zhang, and C. Hellmann, “Approximate solution of Maxwell’s equations by geometrical optics,” Proc. SPIE9630, 963009 (2015).
F. Wyrowski and C. Hellmann, “Geometrical optics reloaded,”Optik Photonik 10, 43–47 (2015).
S. Zhang, D. Asoubar, C. Hellmann, and F. Wyrowski, “Propagation of electromagnetic fields between non-parallel planes: a fully vectorial formulation and an efficient implementation,” Appl. Opt. 55, 529–538 (2016).
34. J. J. Stamnes, B. Spjelkavik, and H. M. Pedersen, “Evaluation of diffraction integrals using local phase and amplitude approximations,”Opt. Acta 30, 207–222 (1983).
D. W. Berreman, “Optics in stratified and anisotropic media:4 × 4-matrix formulation,” J. Opt. Soc. Am. 62, 502–510 (1972).
L. Li, “Reformulation of the Fourier modal method for surface-relief gratings made with anisotropic materials,” J. Mod. Opt. 45,1313–1334 (1998).
L. Li, “Note on the s-matrix propagation algorithm,” J. Opt. Soc. Am. A20, 655–660 (2003).
Z. Wang, “Analytical handling of optical wavefront,” Master’s thesis(Friedrich Schiller University, 2015).
L. Rabiner, R. Schafer, and C. Rader, “The chirp z-transform algorithm,” IEEE Trans. Audio Electroacoust. 17, 86–92 (1969).
J. L. Bakx, “Efficient computation of optical disk readout by use of the chirp z transform,” Appl. Opt. 41, 4897–4903 (2002).
M. Leutenegger, R. Rao, R. A. Leitgeb, and T. Lasser, “Fast focus field calculations,” Opt. Express 14, 11277–11291 (2006).
Physical optics design software, “Wyrowski virtuallab fusion,” developed by Wyrowski Photonics UG, distributed by LightTrans GmbH. http://www.lighttrans.com.
B. L. V. Horn and H. H. Winter, “Analysis of the conoscopic measurement for uniaxial liquid-crystal tilt angles,” Appl. Opt. 40, 2089–2094(2001).
Y. Izdebskaya, E. Brasselet, V. Shvedov, A. Desyatnikov, W.Krolikowski, and Y. Kivshar, “Dynamics of linear polarizationconversion in uniaxial crystals,” Opt. Express 17, 18196–18208(2009).
Y. Qin, Y. Li, X. Feng, Z. Liu, H. He, Y. Xiao, and Q. Gong, “Spin Hall effect of reflected light at the air-uniaxial crystal interface,” Opt.Express 18, 16832–16839 (2010).
P. Ribes-Pleguezuelo, S. Zhang, E. Beckert, R. Eberhardt, F.Wyrowski, and A. Tünnermann, “Method to simulate and analyse induced stresses for laser crystal packaging technologies,” Opt.Express 25, 5927–5940 (2017).
|


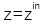 ��
��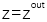 ��ƽ��ƽ�昋(g��u)�ɡ�
��ƽ��ƽ�昋(g��u)�ɡ�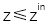 ��
��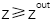 �ą^(q��)���M�ˏ�(f��)�����ʞ�
�ą^(q��)���M�ˏ�(f��)�����ʞ�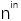 ��
��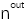 �ľ������ͬ�Խ��|(zh��)�������īI(xi��n)[27]�б���ʹ�ÙM�����Ex��Ey���������������ͬ�Խ��|(zh��)��늴ň�(ch��ng)�ˡ���ˣ��҂�����ʹ�����±��_(d��)ʽ��(l��i)�����ˆ�(w��n)�}��
�ľ������ͬ�Խ��|(zh��)�������īI(xi��n)[27]�б���ʹ�ÙM�����Ex��Ey���������������ͬ�Խ��|(zh��)��늴ň�(ch��ng)�ˡ���ˣ��҂�����ʹ�����±��_(d��)ʽ��(l��i)�����ˆ�(w��n)�}��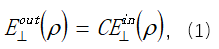
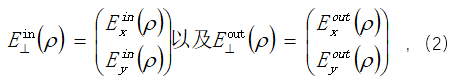
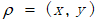 �����̣�1���е�Ԫ��������һ��(g��)2x2�ľ����ʽ��
�����̣�1���е�Ԫ��������һ��(g��)2x2�ľ����ʽ��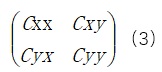
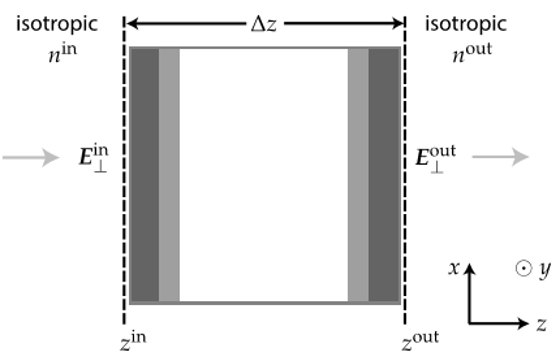
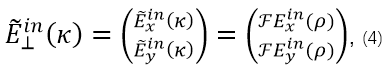
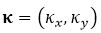 , F��ʾ���S�����~׃�Q��
, F��ʾ���S�����~׃�Q��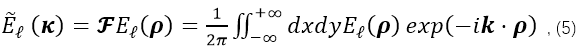
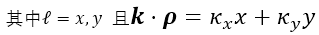 ���渵���~׃�Q���x����
���渵���~׃�Q���x����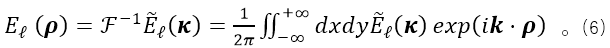
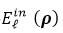 �ֽ����в�ͬ�M��ʸ����κ��ƽ�沨����ˣ����҂�����r�£�ÿ��(g��)ݔ��ƽ�沨�����ԆΪ�(d��)̎��——�҂�����Ӌ(j��)��ÿ��(g��)ݔ��ƽ�沨��ݔ����Ȼ���M(j��n)����͏Ķ��@��ݔ����(ch��ng)��
�ֽ����в�ͬ�M��ʸ����κ��ƽ�沨����ˣ����҂�����r�£�ÿ��(g��)ݔ��ƽ�沨�����ԆΪ�(d��)̎��——�҂�����Ӌ(j��)��ÿ��(g��)ݔ��ƽ�沨��ݔ����Ȼ���M(j��n)����͏Ķ��@��ݔ����(ch��ng)��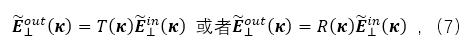
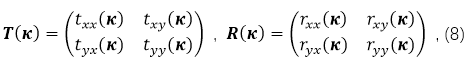
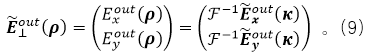
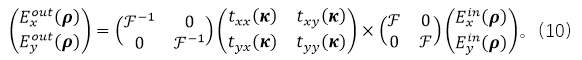
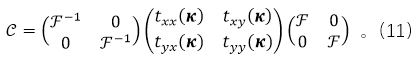
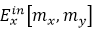 ��
��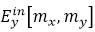 ���ԈD3��a���еľ���W(w��ng)���M(j��n)�вɘӡ��@�N�W(w��ng)���x��
���ԈD3��a���еľ���W(w��ng)���M(j��n)�вɘӡ��@�N�W(w��ng)���x��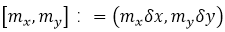 ,����
,����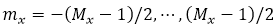 ��
��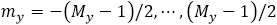 ����������(sh��)��δx��δy��x�����y����IJɘӾ��x����ʼ�ɘӅ���(sh��)��(y��ng)ԓ�ܵ����m�Ŀ�����ʹ����������ǰ���ӵ��ο�˹��-���r(n��ng)�ɘӶ��������̣�10���е�F��(li��n)ϵ���g����l��������ӣ�����ʹ�ò�ͬ�Ĕ�(sh��)ֵ������(sh��)�F(xi��n)����V��ʹ�õĿ��ٸ����~׃�Q��FFT�����g(sh��)���Լ��������܉��M(j��n)һ����ߔ�(sh��)ֵЧ�ʵİ���������~׃�Q[38]�����z׃�Q[39-41]�ĸ���(j��)�ķ������ڴ�ƪ�����У��҂�ʹ����FFT���g(sh��)�����Դ˫@��ݔ����V�����҂����㷨��������ԓ���g(sh��)��
����������(sh��)��δx��δy��x�����y����IJɘӾ��x����ʼ�ɘӅ���(sh��)��(y��ng)ԓ�ܵ����m�Ŀ�����ʹ����������ǰ���ӵ��ο�˹��-���r(n��ng)�ɘӶ��������̣�10���е�F��(li��n)ϵ���g����l��������ӣ�����ʹ�ò�ͬ�Ĕ�(sh��)ֵ������(sh��)�F(xi��n)����V��ʹ�õĿ��ٸ����~׃�Q��FFT�����g(sh��)���Լ��������܉��M(j��n)һ����ߔ�(sh��)ֵЧ�ʵİ���������~׃�Q[38]�����z׃�Q[39-41]�ĸ���(j��)�ķ������ڴ�ƪ�����У��҂�ʹ����FFT���g(sh��)�����Դ˫@��ݔ����V�����҂����㷨��������ԓ���g(sh��)��
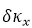 ��
��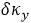 ��ɘӾ��x����b����ʹ��5x5�ɘ��c(di��n)���ش�ֱ��������һ��(g��)�y(c��)ԇ�W(w��ng)��
��ɘӾ��x����b����ʹ��5x5�ɘ��c(di��n)���ش�ֱ��������һ��(g��)�y(c��)ԇ�W(w��ng)��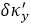 =0.5
=0.5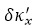 =0.5
=0.5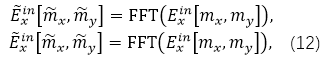
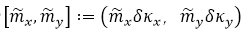 ������
������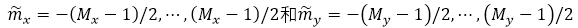 ��
��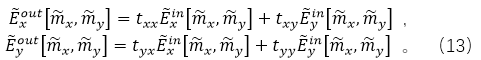
 �IJɘ�ͨ�^(gu��)�����~׃�Q�P(gu��n)ϵ�Ԅ�(d��ng)�_����Ȼ����
�IJɘ�ͨ�^(gu��)�����~׃�Q�P(gu��n)ϵ�Ԅ�(d��ng)�_����Ȼ���� �IJɘӛ](m��i)�б�Ҫ�M(j��n)�д_������?y��n)�����������ϵ�?sh��)��ݔ����V֮�g���c(di��n)�ˡ��@��(g��)��(w��n)�}���ڵ��IJ��ֵİ������M(j��n)��������f(shu��)����
�IJɘӛ](m��i)�б�Ҫ�M(j��n)�д_������?y��n)�����������ϵ�?sh��)��ݔ����V֮�g���c(di��n)�ˡ��@��(g��)��(w��n)�}���ڵ��IJ��ֵİ������M(j��n)��������f(shu��)����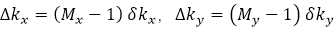 ����M(j��n)���m��(d��ng)�{(di��o)���Դ_�����_�IJɘӡ����҂�����r�У����̣�13���е��\(y��n)��](m��i)�и�׃�V��������ˣ��҂��H�Hֻ��Ҫ�ҵ����m�IJɘӾ��x���ɡ��ˆ�(w��n)�}���](m��i)�н����⣬��?y��n)�ϵ�?sh��)���T����R��ͨ�^(gu��)�f�wS��ꇷ�����(sh��)ֵ�ϫ@�õġ��_��
����M(j��n)���m��(d��ng)�{(di��o)���Դ_�����_�IJɘӡ����҂�����r�У����̣�13���е��\(y��n)��](m��i)�и�׃�V��������ˣ��҂��H�Hֻ��Ҫ�ҵ����m�IJɘӾ��x���ɡ��ˆ�(w��n)�}���](m��i)�н����⣬��?y��n)�ϵ�?sh��)���T����R��ͨ�^(gu��)�f�wS��ꇷ�����(sh��)ֵ�ϫ@�õġ��_��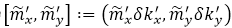 ,����
,����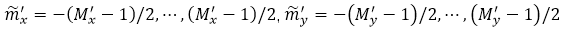 ��ָ��(sh��)�����˲���׃���V������Ҫ��
��ָ��(sh��)�����˲���׃���V������Ҫ��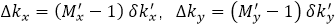 ���c��ʼ�W(w��ng)����ȣ���Ҳ��Ҫ�M(j��n)�м�(x��)�����@��ζ��
���c��ʼ�W(w��ng)����ȣ���Ҳ��Ҫ�M(j��n)�м�(x��)�����@��ζ�� ��
��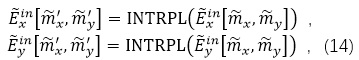
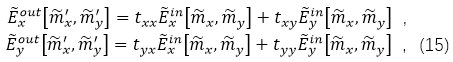
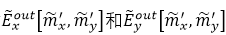 �IJ�ֵ���҂�Ҳ���ԫ@�Üy(c��)ԇ�W(w��ng)���ϵ�ݔ���M����V����������ֵ�Y(ji��)����ʾ��
�IJ�ֵ���҂�Ҳ���ԫ@�Üy(c��)ԇ�W(w��ng)���ϵ�ݔ���M����V����������ֵ�Y(ji��)����ʾ��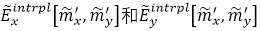 ���҂������^(gu��)��������
���҂������^(gu��)��������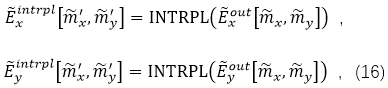
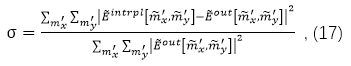
 �ڳ�ʼ�W(w��ng)���ϵIJɘӝM���ο�˹��-���r(n��ng)�ɘӶ��������������IJ�ֵ�Y(ji��)���Ͳ���(hu��)��(du��)��(y��n)��IJ�ֵ�������F(xi��n)��һ��(g��)���ƫ����@�N��r�£�����(j��)���x�IJ�ֵ�������ɷN�Y(ji��)����ƫ�(y��ng)ԓ�ڔ�(sh��)ֵ�`�(j��)�Σ���σ_0��ʾ��ʹ��������(bi��o)��(zh��n)��ͨ�^(gu��)һ�����ĜpС�ɘ��g����(l��i)�y(c��)ԇ��(ch��ng)�ɘӣ�ֱ��σ<σ_0��
�ڳ�ʼ�W(w��ng)���ϵIJɘӝM���ο�˹��-���r(n��ng)�ɘӶ��������������IJ�ֵ�Y(ji��)���Ͳ���(hu��)��(du��)��(y��n)��IJ�ֵ�������F(xi��n)��һ��(g��)���ƫ����@�N��r�£�����(j��)���x�IJ�ֵ�������ɷN�Y(ji��)����ƫ�(y��ng)ԓ�ڔ�(sh��)ֵ�`�(j��)�Σ���σ_0��ʾ��ʹ��������(bi��o)��(zh��n)��ͨ�^(gu��)һ�����ĜpС�ɘ��g����(l��i)�y(c��)ԇ��(ch��ng)�ɘӣ�ֱ��σ<σ_0��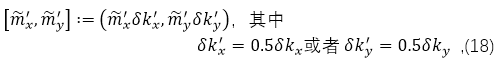
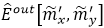 �r(sh��)���H�H��ҪӋ(j��)����Щ�ڿ��ĈAȦλ��̎��ֵ������(sh��)���c(di��n)λ��̎��ֵ��֮ǰ�Ĝy(c��)ԇѭ�h(hu��n)���ѽ�(j��ng)Ӌ(j��)���^(gu��)�ˣ������@Щֵ��(ji��n)�ε��M(j��n)�Ђ�ݔ���ɡ����@�N��ʽ�£��@Щ���ڜy(c��)ԇĿ�����M(j��n)�Ї�(y��n)��Ӌ(j��)���ֵ����(hu��)���G��������(hu��)������һ��ѭ�h(hu��n)�е���ʼ�c(di��n)������ʹ�á���ˣ���һ��(g��)������Ӌ(j��)��������(zh��)�е��LJ�(y��n)���Ӌ(j��)�㣬�Ķ��(y��n)�C���m�IJɘӣ������@ЩӋ(j��)���ֵ�܉���Ч�����ژ�(g��u)����Kݔ����(ch��ng)���҂�������ķ������Y(ji��)���㷨1�С�
�r(sh��)���H�H��ҪӋ(j��)����Щ�ڿ��ĈAȦλ��̎��ֵ������(sh��)���c(di��n)λ��̎��ֵ��֮ǰ�Ĝy(c��)ԇѭ�h(hu��n)���ѽ�(j��ng)Ӌ(j��)���^(gu��)�ˣ������@Щֵ��(ji��n)�ε��M(j��n)�Ђ�ݔ���ɡ����@�N��ʽ�£��@Щ���ڜy(c��)ԇĿ�����M(j��n)�Ї�(y��n)��Ӌ(j��)���ֵ����(hu��)���G��������(hu��)������һ��ѭ�h(hu��n)�е���ʼ�c(di��n)������ʹ�á���ˣ���һ��(g��)������Ӌ(j��)��������(zh��)�е��LJ�(y��n)���Ӌ(j��)�㣬�Ķ��(y��n)�C���m�IJɘӣ������@ЩӋ(j��)���ֵ�܉���Ч�����ژ�(g��u)����Kݔ����(ch��ng)���҂�������ķ������Y(ji��)���㷨1�С�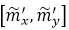
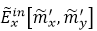
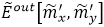
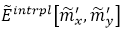
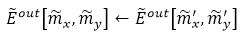 ���t⊳��Ŀǰ��ݔ����(ch��ng)�O(sh��)�Þ���һ��ѭ�h(hu��n)����ʼ�c(di��n)
���t⊳��Ŀǰ��ݔ����(ch��ng)�O(sh��)�Þ���һ��ѭ�h(hu��n)����ʼ�c(di��n)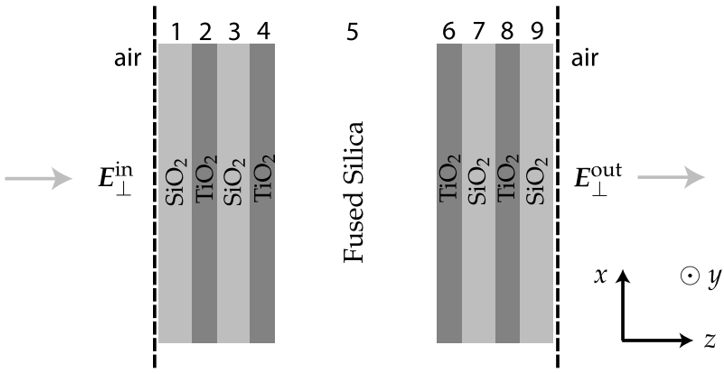

 �IJɘӲ����Ԅ�(d��ng)�õ����C���˰����Ќ��@ʾԓ�F(xi��n)��(bi��o)��(zh��n)���������l���x���ܣ��l�V����l�ʣ����õ��V����ʹ�á����҂��İ����У����l���x����Խ�ጞ�ϵ��(sh��)
�IJɘӲ����Ԅ�(d��ng)�õ����C���˰����Ќ��@ʾԓ�F(xi��n)��(bi��o)��(zh��n)���������l���x���ܣ��l�V����l�ʣ����õ��V����ʹ�á����҂��İ����У����l���x����Խ�ጞ�ϵ��(sh��)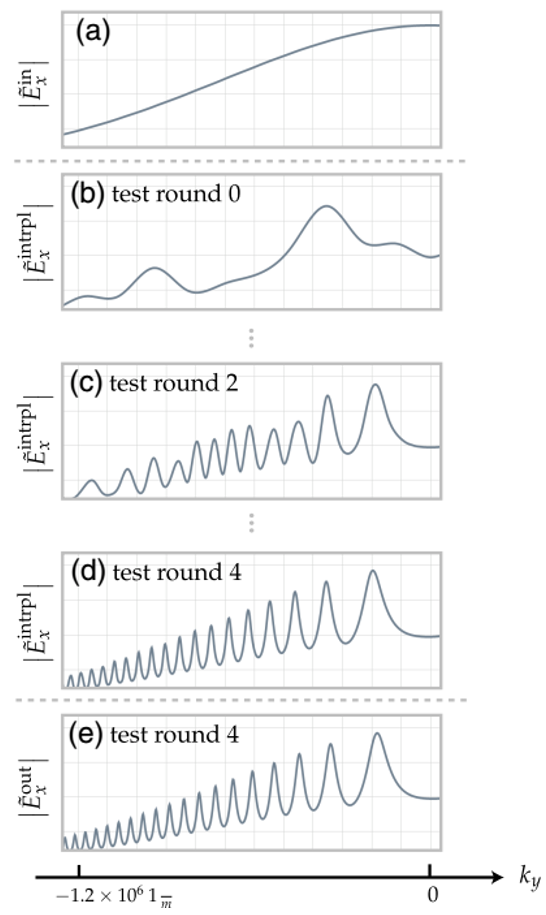
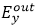 Ҳֵ��ע�⣬�M�������Ҫ�h(yu��n)С��
Ҳֵ��ע�⣬�M�������Ҫ�h(yu��n)С��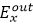 ��Ex��Ey֮�g���F(xi��n)��ƫ��?d��ng)_������ϵ��(sh��)���T����R�ķnj�(du��)����ʽ��ɵġ���
��Ex��Ey֮�g���F(xi��n)��ƫ��?d��ng)_������ϵ��(sh��)���T����R�ķnj�(du��)����ʽ��ɵġ���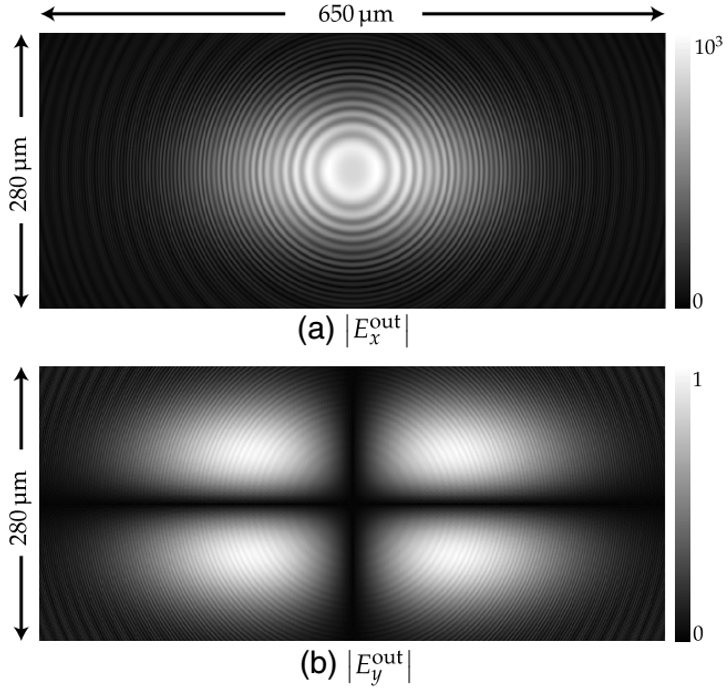
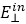 ���f�����w���ǰ���棬������ݔ����(ch��ng)�������������@��(g��)�ӹ�(ji��)�У��҂��](m��i)��ӑՓ���w��Ԫ���ⲿ�^(q��)��Ă������E��
���f�����w���ǰ���棬������ݔ����(ch��ng)�������������@��(g��)�ӹ�(ji��)�У��҂��](m��i)��ӑՓ���w��Ԫ���ⲿ�^(q��)��Ă������E��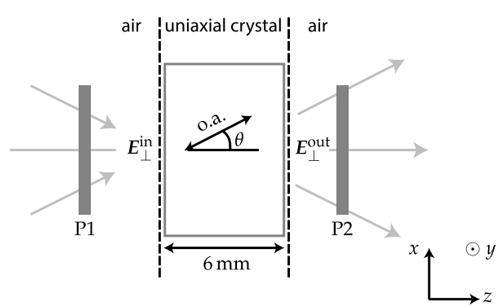



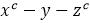 ����(bi��o)ϵ�y(t��ng)��(l��i)��ʾ������S��o.a.����
����(bi��o)ϵ�y(t��ng)��(l��i)��ʾ������S��o.a.����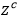 ����ݔ��ͷ����(ch��ng)����
����ݔ��ͷ����(ch��ng)����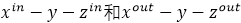 �нo��
�нo��