其中,i,j=1,2,3。二階張量B(0,ij)代表無應力折射率橢球張量,∆Bij代表由于誘導應力產生折射率橢球變化,它可以表示為
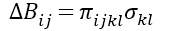
(2)
其中,k,l=1,2,3,愛因斯坦的求和規則在這里適用。二階張量σkl代表了誘導矢量主應力,πijkl是描述每個材料的第四階壓電光學常數張量。通過方程式(1)和(2),當某些壓力σkl產生時,我們可以計算折射率橢球張量Bij。然后,可以用下面的關系式來計算介電常數張量ϵij
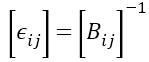
(3)
得到的結果ϵij來進行晶體的后續光學仿真。方程式(1)-(3)在任何坐標系中都成立。然而,需要強調,應用每個方程式的張量時,要用同一坐標系表示。由于晶體材料的對稱性,在晶體坐標系中就很容易描述它們的性質,例如,壓電光學張量πijkl通常只在這樣的系統參考書目中給出[6]。另一方面,在實驗室坐標系中,通過實際的晶體幾何結構可以便捷描述應力σij,為了后續的光學模擬,需要給出介電常數ϵij。更嚴格的,我們首先定義兩個笛卡爾坐標系統x-y-z和x,-y,-z,分別代表實驗室和晶體坐標系統,[aij]作為從實驗室到晶體系統的轉換矩陣。因為應力通常在實驗室系統中用x,y,z來描述,壓電張量通常是在晶體坐標系中用x,y,z,給出。為了使用公式(2),這兩個量必須在相同的坐標系中表示。為了簡易,將二階應力張量轉換到晶體系統,而不是轉換四階壓電張量。由于對稱性,根據Nye’慣例,應力通常以縮寫的方式表達,如σn,n=1,……,6。應用3×3坐標變換矩陣,我們首先將縮寫σn明確為σij,然后使用下面的方程
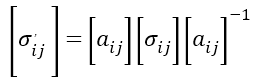
(4)
來計算在晶體系統中關于x,y,z,的應力張量。坐標變換不改變對稱性,根據Nye’慣例,應力張量σij也可以縮寫為σ^,。同樣,由于晶體的對稱性,使用Nye,慣例[6],方程式(2)中的張量可以縮寫,我們可以在晶體坐標系中用x,y,z,改寫方程式(2),如下
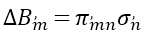
(5)
其中,m,n=1,……6。實際上,壓電光學張量幾乎總是以晶體系統中6×6矩陣的縮寫方式給出。在計算方程式(5)之后,∆Bm^,可以改寫為一個更明確的形式∆Bij^,。
接下來,使用方程式(1),包含應力影響的折射率橢球可以計算出來。由于以下事實:1)由等式(5)得到的張量∆Bij^,在晶體系統中給出; 2)無應力折射率橢球張量在晶體系統中有一個簡單的對角線形式;我們在晶體系統中進行方程式(1)的計算,得到
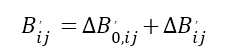
(6)
其中
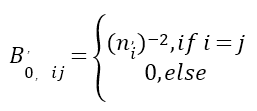
(7)
......


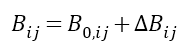 (1)
(1)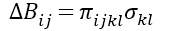 (2)
(2)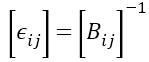 (3)
(3)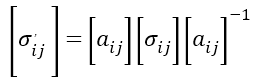 (4)
(4)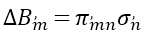 (5)
(5)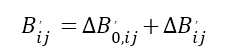 (6)
(6)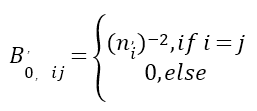 (7)
(7)